某工廠家具車間造A、B型兩類桌子，每張桌子需木工和漆工兩道工序完成.已知木工做一張A、B型桌子分別需要1小時和2小時，漆工油漆一張A、B型桌子分別需要3小時和1小時；又知木工、漆工每天工作分別不得超過8小時和9小時，而工廠造一張A、B型桌子分別獲利潤2千元和3千元，試問工廠每天應生產A、B型桌子各多少張，才能獲得利潤最大？最大利潤是多少？
每天應生產A型桌子2張，B型桌子3張才能獲得最大利潤，最大利潤為13千元.
解析試題分析：設每天生產A型桌子x張，B型桌子y張，根據題意可列出不等式組
在平面直角坐標系中作出上不等式組所表示的平面區域，將目標函數
化成
當
變化時，它表示一組平行直線，當該直線經過可行域且在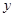
軸上的截距最大時最大.依此找出最優解，求得的最大值.
試題解析：
解：設每天生產A型桌子x張，B型桌子y張，則
目標函數為：z=2x+3y
作出可行域：
把直線
：2x+3y=0向右上方平移至
的位置時，直線經過可行域上的點M，且與原點距離最大，此時z=2x+3y取最大值
解方程
得M的坐標為（2，3）
此時最大利潤
千元
答：每天應生產A型桌子2張，B型桌子3張才能獲得最大利潤，最大利潤為13千元.
考點：線線規劃.
科目：高中數學 來源： 題型：解答題
某企業生產A，B兩種產品，生產每噸產品所需的勞動力和煤、電耗如下表：
已知生產每噸A產品的利潤是7萬元，生產每噸B產品的利潤是12萬元，現因條件限制，該企業僅有勞動力300個，煤360 t，并且供電局只能供電200 kW，試問該企業生產A，B兩種產品各多少噸，才能獲得最大利潤？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某公司承擔了每天至少搬運280噸水泥的任務，已知該公司有6輛A型卡車和8輛B型卡車．又已知A型卡車每天每輛的運載量為30噸，成本費為0.9千元；B型卡車每天每輛的運載量為40噸，成本費為1千元．
（1）如果你是公司的經理，為使公司所花的成本費最小，每天應派出A型卡車、B型卡車各多少輛？
（2）在（1）的所求區域內，求目標函數
的最大值和最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
滿足
則
的最小值是 
，求目標函數z=x+2y+2的最大值和最小值．
的實數 
，不等式 
恒成立，則實數
的最大值是_______.
為任意實數，不等式組
表示區域
，若指數函數
的
的取值范圍是_____________．
滿足
，則
的取值范圍是
（其中
），若不等式有解，則實數a的取值范圍是（ ）
