
已知函數(shù) ,其中
,其中 .
.
(1)若曲線 在點(diǎn)
在點(diǎn) 處的切線方程為
處的切線方程為 ,求函數(shù)
,求函數(shù) 的解析式;
的解析式;
(2)討論函數(shù) 的單調(diào)性;
的單調(diào)性;
(3)若對(duì)于任意的 ,不等式
,不等式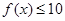 在
在 上恒成立,求
上恒成立,求 的取值范圍.
的取值范圍.
(1)函數(shù) 的解析式為
的解析式為 ;(2)當(dāng)
;(2)當(dāng) 時(shí),
時(shí), 在
在 ,
, 內(nèi)是增函數(shù);當(dāng)
內(nèi)是增函數(shù);當(dāng) 時(shí)
時(shí) 在
在 ,
,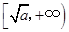 內(nèi)是增函數(shù),在
內(nèi)是增函數(shù),在 ,
, 內(nèi)是減函數(shù);(3)
內(nèi)是減函數(shù);(3) .
.
解析試題分析:(1)先求出導(dǎo)函數(shù)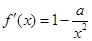 ,進(jìn)而根據(jù)曲線
,進(jìn)而根據(jù)曲線 在點(diǎn)
在點(diǎn) 處的切線方程為
處的切線方程為 得到
得到 即
即 ,從中可求解出
,從中可求解出 的值,進(jìn)而可確定函數(shù)
的值,進(jìn)而可確定函數(shù) 的解析式;(2)針對(duì)導(dǎo)函數(shù),對(duì)
的解析式;(2)針對(duì)導(dǎo)函數(shù),對(duì) 分
分 、
、 兩類,由導(dǎo)數(shù)大于零求出函數(shù)的單調(diào)增區(qū)間,由導(dǎo)數(shù)小于零可求出函數(shù)的單調(diào)遞減區(qū)間;(3)要使對(duì)于任意的
兩類,由導(dǎo)數(shù)大于零求出函數(shù)的單調(diào)增區(qū)間,由導(dǎo)數(shù)小于零可求出函數(shù)的單調(diào)遞減區(qū)間;(3)要使對(duì)于任意的 ,不等式
,不等式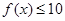 在
在 上恒成立,只須
上恒成立,只須 ,由(2)的討論,確定函數(shù)
,由(2)的討論,確定函數(shù) ,進(jìn)而得到不等式
,進(jìn)而得到不等式 即
即 ,該不等式組對(duì)任意的
,該不等式組對(duì)任意的 成立,從中可求得
成立,從中可求得 .
.
(1)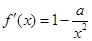 ,由導(dǎo)數(shù)的幾何意義得
,由導(dǎo)數(shù)的幾何意義得 ,于是
,于是
由切點(diǎn) 在直線
在直線 上可得
上可得 ,解得
,解得
所以函數(shù) 的解析式為
的解析式為 3分
3分
(2)因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/28/7/dp5ev1.png" style="vertical-align:middle;" />
當(dāng) 時(shí),顯然
時(shí),顯然 ,這時(shí)
,這時(shí) 在
在 ,
, 內(nèi)是增函數(shù)
內(nèi)是增函數(shù)
當(dāng) 時(shí),令
時(shí),令 ,解得
,解得
當(dāng) 變化時(shí),
變化時(shí), ,
, 的變化情況如下表:
的變化情況如下表: