
設橢圓C1的方程為![]() (a>b>0),曲線C2的方程為y=
(a>b>0),曲線C2的方程為y=![]() ,且曲線C1與C2在第一象限內只有一個公共點P.
,且曲線C1與C2在第一象限內只有一個公共點P.
(1)試用a表示點P的坐標;
(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;
(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個. 設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式.
(1)P的坐標為(![]() )(2)△ABP的面積函數S(a)的值域為(0,
)(2)△ABP的面積函數S(a)的值域為(0,![]() )(3)f(a)=min{g(a), S(a)}
)(3)f(a)=min{g(a), S(a)}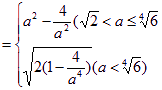
(1)將y=![]() 代入橢圓方程,得
代入橢圓方程,得![]()
化簡,得b2x4–a2b2x2+a2=0
由條件,有Δ=a4b4–4a2b2=0,得ab=2
解得x=![]() 或x=–
或x=–![]() (舍去)故P的坐標為(
(舍去)故P的坐標為(![]() ).
).
(2)∵在△ABP中,|AB|=2![]() ,高為
,高為![]() ,
,
∴![]()
∵a>b>0,b=![]()
∴a>![]() ,即a>
,即a>![]() ,得0<
,得0<![]() <1
<1
于是0<S(a)<![]() ,故△ABP的面積函數S(a)的值域為(0,
,故△ABP的面積函數S(a)的值域為(0,![]() )
)
(3)g(a)=c2=a2–b2=a2–![]()
解不等式g(a)≥S(a),即a2–![]() ≥
≥![]()
整理,得a8–10a4+24≥0,即(a4–4)(a4–6)≥0
解得a≤![]() (舍去)或a≥
(舍去)或a≥![]()
![]()
故f(a)=min{g(a), S(a)}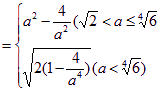


科目:高中數學 來源:數學教研室 題型:044
(Ⅰ)試用a表示點P的坐標.
(Ⅱ)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;
(Ⅲ)設min{y1,y2,…,yn}為y1,y2,…,yn中最小的一個.設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,求函數f(a)=min{g(a),S(a)}的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)設橢圓C1的方程為![]() (a>b>0),曲線C2的方程為y=
(a>b>0),曲線C2的方程為y=![]() ,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
,且曲線C1與C2在第一象限內只有一個公共點P。(1)試用a表示點P的坐標;(2)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;(3)記min{y1,y2,……,yn}為y1,y2,……,yn中最小的一個。設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試求函數f(a)=min{g(a), S(a)}的表達式。
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)試用a表示點P的坐標.
(Ⅱ)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;
(Ⅲ)設min{y1,y2,…,yn}為y1,y2,…,yn中最小的一個設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試函數f(a)=min{g(a),S(a)}的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
(Ⅰ)試用a表示點P的坐標.
(Ⅱ)設A、B是橢圓C1的兩個焦點,當a變化時,求△ABP的面積函數S(a)的值域;
(Ⅲ)設min{y1,y2,…,yn}為y1,y2,…,yn中最小的一個設g(a)是以橢圓C1的半焦距為邊長的正方形的面積,試函數f(a)=min{g(a),S(a)}的表達式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com