Question

【題目】如圖，將邊長為1的正方形沿對角線折起，使得平面平面，在折起后形成的三棱錐中，給出下列四種說法：

①是等邊三角形；②；③；④直線和所成的角的大小為．其中所有正確的序號是（ ）

A. ①③B. ②④C. ①②③D. ①②④

Answer 1

【答案】D

【解析】

①取中點，連接中點，則，利用面面垂直的性質定理可證得平面，利用線面垂直性質可得，利用勾股定理求得，可知①正確；對于②，因為，，利用線面垂直判定定理可知平面，根據線面垂直性質可知；對于③可以采用反證法進行否定；對于④，以為坐標原點建立空間坐標系，利用空間向量法求解向量的夾角．

對于①，因為，取中點，連接，

則，，

平面平面，平面平面 平面

在中，，故①正確；

對于②，由①，知，，又 平面

又平面 ，故②正確；

對于③，假設；又， 平面

平面

又， 平面

這與空間中過一點有且只有一條直線與一個平面垂直矛盾，故③錯誤；

對于④，以為坐標原點，為軸，，分別為軸，軸，建立坐標系

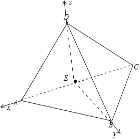
則，，，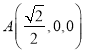

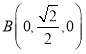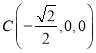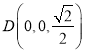
所以，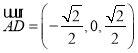

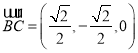
設直線和所成的角為，則

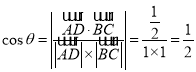
．故④正確．

本題正確選項：