Question

【題目】函數(shù)是定義在上的奇函數(shù)，且為偶函數(shù)，當時，，若函數(shù)恰有一個零點，則實數(shù)的取值范圍是

A. B.

C. D.

Answer 1

【答案】D

【解析】分析：根據(jù)條件判斷函數(shù)的周期性和對稱性，求出函數(shù)在一個周期內(nèi)的解析式，利用轉(zhuǎn)化法進行求解即可．

詳解：∵f（x）是定義在R上的奇函數(shù)，且f（x﹣1）為偶函數(shù)，

∴f（﹣x﹣1）=f（x﹣1）=﹣f（x+1），

即f（x）=﹣f（x+2），

則f（x+4）=﹣f（x+2）=f（x），即函數(shù)f（x）的周期是4，

∵f（x﹣1）為偶函數(shù)，∴f（x﹣1）關于x=0對稱，

則f（x）關于x=﹣1對稱，同時也關于x=1對稱，

若x∈[﹣1，0]，則﹣x∈[0，1]，

此時f（﹣x）==﹣f（x），則f（x）=﹣，x∈[﹣1，0]，

若x∈[﹣2，﹣1]，x+2∈[0，1]，

則f（x）=﹣f（x+2）=﹣，x∈[﹣2，﹣1]，

若x∈[1，2]，x﹣2∈[﹣1，0]，

則f（x）=﹣f（x﹣2）==，x∈[1，2]，

作出函數(shù)f（x）的圖象如圖：

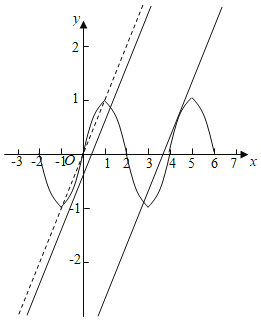
由數(shù)g（x）=f（x）﹣x﹣b=0得f（x）=x+b，

由圖象知當x∈[﹣1，0]時，由﹣=x+b，平方得x2+（2b+1）x+b2=0，

由判別式△=（2b+1）2﹣4b2=0得4b+1=0，得b=﹣，此時f（x）=x+b有兩個交點，

當x∈[4，5]，x﹣4∈[0，1]，則f（x）=f（x﹣4）=，

由=x+b，平方得x2+（2b﹣1）x+4+b2=0，

由判別式△=（2b﹣1）2﹣16﹣4b2=0得4b=﹣15，得b=﹣，此時f（x）=x+b有兩個交點，

則要使此時f（x）=x+b有一個交點，則在[0，4]內(nèi)，b滿足﹣＜b＜﹣，

即實數(shù)b的取值集合是4n﹣＜b＜4n﹣，

即4（n﹣1）+＜b＜4（n﹣1）+，

令k=n﹣1，

則4k+＜b＜4k+，

故選：D．