
【題目】對(duì)數(shù)列![]() ,規(guī)定
,規(guī)定![]() 為數(shù)列
為數(shù)列![]() 的一階差分?jǐn)?shù)列,其中
的一階差分?jǐn)?shù)列,其中![]() ,規(guī)定
,規(guī)定![]() 為
為![]() 的二階差分?jǐn)?shù)列,其中
的二階差分?jǐn)?shù)列,其中![]() .
.
(1)數(shù)列![]() 的通項(xiàng)公式
的通項(xiàng)公式![]() ,試判斷
,試判斷![]() ,
,![]() 是否為等差數(shù)列,請(qǐng)說明理由?
是否為等差數(shù)列,請(qǐng)說明理由?
(2)數(shù)列![]() 是公比為
是公比為![]() 的正項(xiàng)等比數(shù)列,且
的正項(xiàng)等比數(shù)列,且![]() ,對(duì)于任意的
,對(duì)于任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,求
,求![]() 所有可能的取值構(gòu)成的集合;
所有可能的取值構(gòu)成的集合;
(3)各項(xiàng)均為正數(shù)的數(shù)列![]() 的前
的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,且
,且![]() ,對(duì)滿足
,對(duì)滿足![]() ,
,![]() 的任意正整數(shù)
的任意正整數(shù)![]() 、
、![]() 、
、![]() ,都有
,都有![]() ,且不等式
,且不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的最大值.
的最大值.
【答案】(1)![]() ,
,![]() 是等差數(shù)列,見解析(2)
是等差數(shù)列,見解析(2)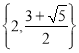 ;(3)2
;(3)2
【解析】
(1)根據(jù)題干中的定義,結(jié)合等差數(shù)列的定義即可判斷.
(2)根據(jù)等比數(shù)列的通項(xiàng)公式可得![]() ,結(jié)合題干可得
,結(jié)合題干可得![]() ,從而可得
,從而可得![]() ,且
,且![]() ;分類討論
;分類討論![]() 、
、![]() 或
或![]() 即可求出
即可求出![]() .
.
(3)根據(jù)題中對(duì)數(shù)列的定義可得![]()
![]() ,從而可得
,從而可得![]() ,即
,即![]() 是等差數(shù)列,根據(jù)數(shù)列為正項(xiàng)等差數(shù)列可得
是等差數(shù)列,根據(jù)數(shù)列為正項(xiàng)等差數(shù)列可得![]() ,代入等差數(shù)列前
,代入等差數(shù)列前![]() 項(xiàng)和公式,由
項(xiàng)和公式,由![]() ,可得
,可得![]() ,當(dāng)
,當(dāng)![]() 時(shí),不等式
時(shí),不等式![]() 都成立;當(dāng)
都成立;當(dāng)![]() 時(shí),令
時(shí),令![]() ,
,![]() ,代入等差數(shù)列的前
,代入等差數(shù)列的前![]() 項(xiàng)和公式,作差
項(xiàng)和公式,作差![]() ,由
,由![]() ,
,![]() ,即可求解.
,即可求解.
解:(1)因?yàn)?/span>![]() ,所以
,所以![]() ,
,
則![]() ,又
,又![]() ,所以
,所以![]() 是首項(xiàng)為3,公差為2的等差數(shù)列.
是首項(xiàng)為3,公差為2的等差數(shù)列.
因?yàn)?/span>![]() ,則
,則![]() 是首項(xiàng)為2,公差為0的等差數(shù)列.
是首項(xiàng)為2,公差為0的等差數(shù)列.
(2)因?yàn)閿?shù)列![]() 是公比為
是公比為![]() 的正項(xiàng)等比數(shù)列,所以
的正項(xiàng)等比數(shù)列,所以![]() .
.
又![]() ,
,
且對(duì)任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
所以對(duì)任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() ,
,
即![]() ,因?yàn)?/span>
,因?yàn)?/span>![]() ,所以
,所以![]() .
.
![]() 若
若![]() ,則
,則![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
即當(dāng)![]() 時(shí),對(duì)任意的
時(shí),對(duì)任意的![]() ,都有
,都有![]() .
.
![]() 若
若![]() ,則
,則![]() ,解得
,解得![]() (舍)或
(舍)或![]() ,
,
即當(dāng)![]() 時(shí),對(duì)任意的
時(shí),對(duì)任意的![]() ,都有
,都有![]() .
.
![]() 若
若![]() ,則
,則![]() ,
,
故對(duì)任意的![]() ,不存在
,不存在![]() ,使得
,使得![]() .
.
綜上所述,![]() 所有可能的取值構(gòu)成的集合為
所有可能的取值構(gòu)成的集合為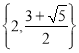 ;
;
(3)因?yàn)?/span>![]() ,所以
,所以![]()
![]() ,
,
則![]() ,所以
,所以![]() 是等差數(shù)列.
是等差數(shù)列.
設(shè)![]() 的公差為
的公差為![]() ,則
,則![]() .
.
若![]() ,則
,則![]() ;
;
若![]() ,則當(dāng)
,則當(dāng)![]() 時(shí),
時(shí),![]() ,
,
與數(shù)列![]() 的各項(xiàng)均為正數(shù)矛盾,故
的各項(xiàng)均為正數(shù)矛盾,故![]() .
.
由等差數(shù)列前![]() 項(xiàng)和公式可得
項(xiàng)和公式可得![]() ,
,
所以![]()
![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,
所以![]()
![]() ,
,
則當(dāng)![]() 時(shí),不等式
時(shí),不等式![]() 都成立.
都成立.
另一方面,當(dāng)![]() 時(shí),令
時(shí),令![]() ,
,![]() ,
,
則![]()
![]() ,
,
![]() ,
,
則![]()
![]() ,
,
因?yàn)?/span>![]() ,
,![]() ,
,
所以當(dāng)![]() 時(shí),
時(shí),![]() ,即
,即![]() .不滿足任意性.
.不滿足任意性.
所以![]() .
.
綜上,![]() 的最大值為2.
的最大值為2.


 科學(xué)實(shí)驗(yàn)活動(dòng)冊(cè)系列答案
科學(xué)實(shí)驗(yàn)活動(dòng)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2020年春,新型冠狀病毒在我國湖北武漢爆發(fā)并訊速蔓延,病毒傳染性強(qiáng)并嚴(yán)重危害人民生命安全,國家衛(wèi)健委果斷要求全體人民自我居家隔離,為支援湖北武漢新型冠狀病毒疫情防控工作,各地醫(yī)護(hù)人員紛紛逆行,才使得病毒蔓延得到了有效控制.某社區(qū)為保障居民的生活不受影響,由社區(qū)志愿者為其配送蔬菜、大米等生活用品,記者隨機(jī)抽查了男、女居民各100名對(duì)志愿者所買生活用品滿意度的評(píng)價(jià),得到下面的2×2列聯(lián)表.
特別滿意 | 基本滿意 | |
男 | 80 | 20 |
女 | 95 | 5 |
(1)被調(diào)查的男性居民中有5個(gè)年輕人,其中有2名對(duì)志愿者所買生活用品特別滿意,現(xiàn)在這5名年輕人中隨機(jī)抽取3人,求至多有1人特別滿意的概率.
(2)能否有99%的把握認(rèn)為男、女居民對(duì)志愿者所買生活用品的評(píng)價(jià)有差異?
附: 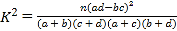
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,曲線C1的參數(shù)方程為![]() (θ為參數(shù)),以原點(diǎn)為極點(diǎn),x軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線C2的極坐標(biāo)方程為
(θ為參數(shù)),以原點(diǎn)為極點(diǎn),x軸非負(fù)半軸為極軸,建立極坐標(biāo)系,曲線C2的極坐標(biāo)方程為![]() .
.
(1)求曲線C1的極坐標(biāo)方程以及曲線C2的直角坐標(biāo)方程;
(2)若直線l:y=kx與曲線C1、曲線C2在第一象限交于P、Q,且|OQ|=|PQ|,點(diǎn)M的直角坐標(biāo)為(1,0),求△PMQ的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在正方體![]() 中,棱長為2,
中,棱長為2,![]() 分別為棱
分別為棱![]() 的中點(diǎn),
的中點(diǎn),![]() 為底面正方形
為底面正方形![]() 內(nèi)一點(diǎn)(含邊界)且
內(nèi)一點(diǎn)(含邊界)且![]() 與面
與面![]() 所成角的正切值為
所成角的正切值為![]() ,直線
,直線![]() 與面
與面![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,當(dāng)
,當(dāng)![]() 到
到![]() 的距離最小時(shí),則四面體
的距離最小時(shí),則四面體![]() 外接球的表面積為___________.
外接球的表面積為___________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系xOy中,直線l的參數(shù)方程為![]() (t為參數(shù)),若以O為極點(diǎn),x軸的正半軸為極軸且取相同的單位長度建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為
(t為參數(shù)),若以O為極點(diǎn),x軸的正半軸為極軸且取相同的單位長度建立極坐標(biāo)系,曲線C的極坐標(biāo)方程為![]() .
.
(1)求曲線C的直角坐標(biāo)方程及直線l的普通方程;
(2)將所得曲線C向右平移1個(gè)單位長度,再將曲線C上的所有點(diǎn)的橫坐標(biāo)變?yōu)樵瓉淼?/span>2倍,得到曲線![]() ,求曲線
,求曲線![]() 上的點(diǎn)到直線l的距離的最大值.
上的點(diǎn)到直線l的距離的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若曲線![]() 在點(diǎn)
在點(diǎn)![]() 處的切線斜率為1,求實(shí)數(shù)a的值;
處的切線斜率為1,求實(shí)數(shù)a的值;
(2)當(dāng)![]() 時(shí),求證:
時(shí),求證:![]() ;
;
(3)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上存在極值點(diǎn),求實(shí)數(shù)a的取值范圍.
上存在極值點(diǎn),求實(shí)數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】《九章算術(shù)》中“勾股容方”問題:“今有勾五步,股十二步,問勾中容方幾何?”魏晉時(shí)期數(shù)學(xué)家劉徽在其《九章算術(shù)注》中利用出入相補(bǔ)原理給出了這個(gè)問題的一般解法:如圖1,用對(duì)角線將長和寬分別為![]() 和
和![]() 的矩形分成兩個(gè)直角三角形,每個(gè)直角三角形再分成一個(gè)內(nèi)接正方形(黃)和兩個(gè)小直角三角形(朱、青).將三種顏色的圖形進(jìn)行重組,得到如圖2所示的矩形.該矩形長為
的矩形分成兩個(gè)直角三角形,每個(gè)直角三角形再分成一個(gè)內(nèi)接正方形(黃)和兩個(gè)小直角三角形(朱、青).將三種顏色的圖形進(jìn)行重組,得到如圖2所示的矩形.該矩形長為![]() ,寬為內(nèi)接正方形的邊長
,寬為內(nèi)接正方形的邊長![]() .由劉徽構(gòu)造的圖形還可以得到許多重要的結(jié)論,如圖3.設(shè)
.由劉徽構(gòu)造的圖形還可以得到許多重要的結(jié)論,如圖3.設(shè)![]() 為斜邊
為斜邊![]() 的中點(diǎn),作直角三角形
的中點(diǎn),作直角三角形![]() 的內(nèi)接正方形對(duì)角線
的內(nèi)接正方形對(duì)角線![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 于點(diǎn)
于點(diǎn)![]() ,則下列推理正確的是( )
,則下列推理正確的是( )
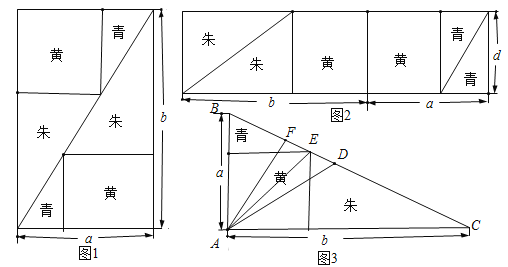
①由圖1和圖2面積相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得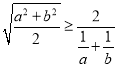 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,其中
,其中![]() 是自然對(duì)數(shù)的底數(shù),
是自然對(duì)數(shù)的底數(shù),![]() 是函數(shù)
是函數(shù)![]() 的導(dǎo)數(shù).
的導(dǎo)數(shù).
(1)若![]() 是
是![]() 上的單調(diào)函數(shù),求
上的單調(diào)函數(shù),求![]() 的值;
的值;
(2)當(dāng)![]() 時(shí),求證:若
時(shí),求證:若![]() ,且
,且![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列結(jié)論中正確的個(gè)數(shù)是( )
①在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
②若![]() ,
,![]() 的最小值為2;
的最小值為2;
③夾在圓柱的兩個(gè)平行截面間的幾何體是圓柱;
④數(shù)列![]() 的通項(xiàng)公式為
的通項(xiàng)公式為![]() ,則數(shù)列的前
,則數(shù)列的前![]() 項(xiàng)和
項(xiàng)和![]() .( )
.( )
A.0B.1C.2D.3
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com