
已知函數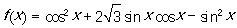
(1)求函數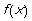 的最小正周期及單調遞增區間;
的最小正周期及單調遞增區間;
(2)在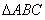 中,A、B、C分別為三邊
中,A、B、C分別為三邊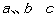 所對的角,若
所對的角,若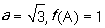 ,求
,求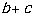 的最大值.
的最大值.
(1)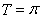 ,函數的單調遞增區間為
,函數的單調遞增區間為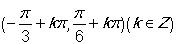 ;(2)因此
;(2)因此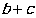 的最大值為
的最大值為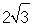 .
.
【解析】
試題分析:(1)將函數 的解析式第一、三項結合,利用二倍角的余弦函數公式化簡,第二項利用二倍角的正弦函數公式化簡,合并后提取
的解析式第一、三項結合,利用二倍角的余弦函數公式化簡,第二項利用二倍角的正弦函數公式化簡,合并后提取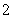 ,再利用兩角和與差的正弦函數公式及特殊角的三角函數值化為一個角的正弦函數,找出
,再利用兩角和與差的正弦函數公式及特殊角的三角函數值化為一個角的正弦函數,找出 的值,代入周期公式
的值,代入周期公式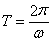 ,即可求出函數的最小正周期,由正弦函數的遞增區間列出關于
,即可求出函數的最小正周期,由正弦函數的遞增區間列出關于 的不等式,求出不等式的解集即可得到
的不等式,求出不等式的解集即可得到 的遞增區間;(2)由
的遞增區間;(2)由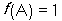 及確定出的
及確定出的 的解析式,變形后利用特殊角的三角函數值求出
的解析式,變形后利用特殊角的三角函數值求出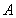 的度數,可得出
的度數,可得出 的值,再由
的值,再由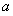 的值,利用余弦定理列出關系式,將
的值,利用余弦定理列出關系式,將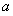 與
與 的值代入,利用完全平方公式變形后,再利用基本不等式即可求出
的值代入,利用完全平方公式變形后,再利用基本不等式即可求出 的最大值.
的最大值.
試題解析:(1)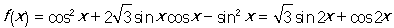
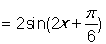 , 3分
, 3分
所以函數的最小正周期為 . 4分
. 4分
由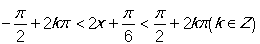 得
得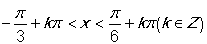
所以函數的單調遞增區間為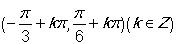 . 6分
. 6分
(2)由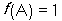 可得
可得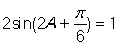 ,又
,又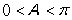 ,所以
,所以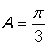 。 8分
。 8分
由余弦定理可得 ,即
,即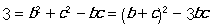 又
又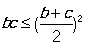 ,所以
,所以 ,故
,故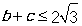 ,當且僅當
,當且僅當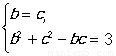 ,即
,即 時等號成立
時等號成立
因此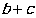 的最大值為
的最大值為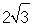 . 12分
. 12分
考點:解三角形;三角函數的化簡求值;三角函數的周期性及其求法;正弦函數的單調性.


科目:高中數學 來源: 題型:
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| π |
| 12 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2008-2009學年湖北省仙桃一中高三(上)第二次段考數學試卷(理科)(解析版) 題型:解答題


查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省棗莊市高三上學期期末檢測理科數學 題型:解答題
(本題滿分12分)
已知函數
(1)求函數 的極值點;
的極值點;
(2)若直線 過點(0,—1),并且與曲線
過點(0,—1),并且與曲線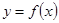 相切,求直線
相切,求直線 的方程;
的方程;
(3)設函數 ,其中
,其中 ,求函數
,求函數 在
在 上的最小值.(其中e為自然對數的底數)
上的最小值.(其中e為自然對數的底數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com