
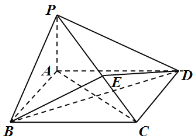
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 為矩形,
為矩形,![]() 平面
平面![]() ,點
,點![]() 在線段
在線段![]() 上,
上,![]() 平面
平面![]() .
.
(Ⅰ)證明:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() ,求二面角
,求二面角![]() 的正切值.
的正切值.
【答案】(1)見解析 ; (2)3 .
【解析】
試題分析: (1)證明線面垂直,一般利用線面垂直判定及性質定理,經多次轉化得證:先由線面垂直PA⊥平面ABCD得線線垂直PA⊥BD.同理PC⊥BD.,再由線線垂直得線面垂直BD⊥平面PAC. (2)求二面角正切值,一般利用空間直角坐標系,根據空間向量數量積進行求解:先建立恰當直角坐標系,設各點坐標,利用方程組得兩平面法向量,再根據向量數量積求其夾角余弦值,最后根據同角三角函數關系求正切值.
試題解析:(1)證明 ∵PA⊥平面ABCD,BD平面ABCD,
∴PA⊥BD.
同理由PC⊥平面BDE,可證得PC⊥BD.
又PA∩PC=P,∴BD⊥平面PAC.
(2)解
如圖,

分別以射線AB,AD,AP為x軸、y軸、z軸的正半軸建立空間直角坐標系.
由(1)知BD⊥平面PAC,
又AC平面PAC,∴BD⊥AC.
故矩形ABCD為正方形,
∴AB=BC=CD=AD=2.
∴A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0),P(0,0,1).
∴![]() =(2,0,-1),
=(2,0,-1),![]() =(0,2,0),
=(0,2,0),![]() =(-2,2,0).
=(-2,2,0).
設平面PBC的一個法向量為n=(x,y,z),則
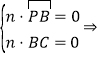
![]()
∴取x=1得n=(1,0,2).
∵BD⊥平面PAC,
∴![]() =(-2,2,0)為平面PAC的一個法向量.
=(-2,2,0)為平面PAC的一個法向量.
cos<n,![]() >=
>=![]()
設二面角B-PC-A的平面角為α,由圖知0<α<![]() ,
,
∴cos α=![]() ,sin α=
,sin α=![]()
∴tan α=![]() =3,即二面角B-PC-A的正切值為3.
=3,即二面角B-PC-A的正切值為3.


科目:高中數學 來源: 題型:
【題目】下圖是我國2008年至2014年生活垃圾無害化處理量(單位:億噸)的折線圖.

(Ⅰ)由折線圖看出,可用線性回歸模型擬合y與t的關系,請用相關系數加以說明;
(Ⅱ)建立y關于t的回歸方程(系數精確到0.01),預測2016年我國生活垃圾無害化處理量.
附注:
參考數據:![]() ,
,![]() ,
,
![]() ,
,![]() ≈2.646.
≈2.646.
參考公式:相關系數
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=ax3﹣3x2+1(a>0),定義h(x)=max{f(x),g(x)}= ![]() .
.
(1)求函數f(x)的極值;
(2)若g(x)=xf'(x),且存在x∈[1,2]使h(x)=f(x),求實數a的取值范圍;
(3)若g(x)=lnx,試討論函數h(x)(x>0)的零點個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() .
.
(Ⅰ)若圓![]() 的切線在
的切線在![]() 軸和
軸和![]() 軸上的截距相等,求此切線的方程;
軸上的截距相等,求此切線的方程;
(Ⅱ)從圓![]() 外一點
外一點![]() 向該圓引一條切線,切點為
向該圓引一條切線,切點為![]() ,
,![]() 為坐標原點,且
為坐標原點,且![]() ,求使
,求使![]() 取得最小值的點
取得最小值的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{xn}滿足x1=0,xn+1=﹣x2n+xn+c(n∈N*).
(Ⅰ)證明:{xn}是遞減數列的充分必要條件是c<0;
(Ⅱ)求c的取值范圍,使{xn}是遞增數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩點M(﹣3,0),N(3,0),點P為坐標平面內一動點,且![]() ,則動點P(x,y)到兩點A(﹣3,0)、B(﹣2,3)的距離之和的最小值為( )
,則動點P(x,y)到兩點A(﹣3,0)、B(﹣2,3)的距離之和的最小值為( )
A. 4 B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}是遞減數列,前n項的積為Tn,若T13=4T9,則a8a15=( )
A. 2 B. ±2 C. 4 D. ±4
【答案】A
【解析】
由題意可得 q>1,且 an >0,由條件可得 a1a2…a13=4a1a2…a9,化簡得a10a11a12a13=4,再由 a8a15=a10a13=a11a12,求得a8a15的值.
等比數列{an}是遞增數列,其前n項的積為Tn(n∈N*),若T13=4T9 ,設公比為q,
則由題意可得 q>1,且 an >0.
∴a1a2…a13=4a1a2…a9,∴a10a11a12a13=4.
又由等比數列的性質可得 a8a15=a10a13=a11a12,∴a8a15=2.
故選:A.
【點睛】
本題主要考查等比數列的定義和性質,求得 a10a11a12a13=4是解題的關鍵.
【題型】單選題
【結束】
10
【題目】若直線y=2x上存在點(x,y)滿足約束條件 ,則實數m的最大值為
,則實數m的最大值為
A. -1 B. 1 C. ![]() D. 2
D. 2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長AB=AD=2,AA1=3的長方體ABCDA1B1C1D1中,點E是平面BCC1B1上的動點,點F是CD的中點.試確定點E的位置,使D1E⊥平面AB1F.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com