
【題目】如圖,在Rt![]() 中,
中,![]() ,點
,點![]() 、
、![]() 分別在線段
分別在線段![]() 、
、![]() 上,且
上,且![]() ,將
,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得二面角
的位置,使得二面角![]() 的大小為
的大小為![]() .
.
(1)求證:![]() ;
;
(2)當點![]() 為線段
為線段![]() 的靠近
的靠近![]() 點的三等分點時,求
點的三等分點時,求![]() 與平面
與平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
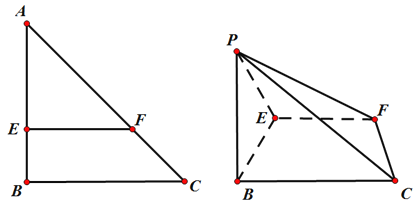
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)由等腰三角形的性質可得![]() ,
,![]() ,翻折后垂直關系沒變,仍有
,翻折后垂直關系沒變,仍有![]() ,
,![]() 平面
平面![]() ,從而得
,從而得![]() ; (2)
; (2) ![]() 二面角
二面角![]() 的平面角,由余弦定理得
的平面角,由余弦定理得![]() ,由勾股定理可得
,由勾股定理可得![]() ,
,![]() 兩兩垂直,以
兩兩垂直,以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系,求出平面
軸,建立空間直角坐標系,求出平面![]() 的法向量與
的法向量與![]() 的方向向量,利用空間向量夾角余弦公式可得結果.
的方向向量,利用空間向量夾角余弦公式可得結果.
試題解析:(1)![]()
![]()
![]()
![]()
![]()
![]() ,翻折后垂直關系沒變,仍有
,翻折后垂直關系沒變,仍有![]() ,
,![]()
![]()
![]() .
.
(2) ![]()
![]() ,
,![]()
![]() 二面角
二面角![]() 的平面角,
的平面角,
![]() ,又
,又![]() ,由余弦定理得
,由余弦定理得![]() ,
,
![]() ,
,![]() ,
,![]() 兩兩垂直.
兩兩垂直.
以![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立如圖直角坐標系.
軸,建立如圖直角坐標系.
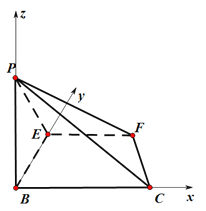
則![]()
![]()
![]()
![]()
![]()
設平面![]() 的法向量
的法向量![]()
由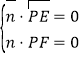 可得
可得![]()
![]()
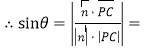
![]() .
.
故PC與平面PEF所成的角的正弦值為 ![]() .
.
【方法點晴】本題主要考查利用空間向量求線面角,屬于難題.空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當?shù)目臻g直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數(shù)量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知直線y=x+b與函數(shù)f(x)=ln x的圖象交于兩個不同的點A,B,其橫坐標分別為x1,x2,且x1<x2.
(1)求b的取值范圍;
(2)當x2≥2時,證明x1·![]() <2.
<2.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知![]() 是拋物線
是拋物線![]() 上的兩個點,點
上的兩個點,點![]() 的坐標為
的坐標為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() .設拋物線
.設拋物線![]() 的焦點在直線
的焦點在直線![]() 的下方.
的下方.
(Ⅰ)求k的取值范圍;
(Ⅱ)設C為W上一點,且![]() ,過
,過![]() 兩點分別作W的切線,記兩切線的交點為
兩點分別作W的切線,記兩切線的交點為![]() . 判斷四邊形
. 判斷四邊形![]() 是否為梯形,并說明理由.
是否為梯形,并說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】選修4-4:坐標系與參數(shù)方程
在平面直角坐標系中,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,已知曲線
軸的正半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,過點
,過點![]() 的直線
的直線![]() 的參數(shù)方程為
的參數(shù)方程為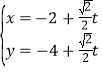 (
(![]() 為參數(shù)),直線
為參數(shù)),直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點.
兩點.
(1)寫出曲線![]() 的直角坐標方程和直線
的直角坐標方程和直線![]() 的普通方程;
的普通方程;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 離心率為
離心率為![]() ,兩準線之間的距離為8,點
,兩準線之間的距離為8,點![]() 在橢圓
在橢圓![]() 上,且位于第一象限,過點
上,且位于第一象限,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若直線![]() 的交點
的交點![]() 在橢圓
在橢圓![]() 上,求點
上,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知圓![]() 與直線
與直線![]() 相切.
相切.
(1)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,求
兩點,求![]() ;
;
(2)設圓![]() 與
與![]() 軸的負半軸的交點為
軸的負半軸的交點為![]() ,過點
,過點![]() 作兩條斜率分別為
作兩條斜率分別為![]() 的直線交圓
的直線交圓![]() 于
于![]() 兩點,且
兩點,且![]() ,試證明直線
,試證明直線![]() 恒過一定點,并求出該定點的坐標.
恒過一定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某學校運動會的立定跳遠和30秒跳繩兩個單項比賽分成預賽和決賽兩個階段.下表為10名學生的預賽成績,其中有三個數(shù)據模糊.
學生序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳遠(單位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳繩(單位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在這10名學生中,進入立定跳遠決賽的有8人,同時進入立定跳遠決賽和30秒跳繩決賽的有6人,則
(A)2號學生進入30秒跳繩決賽
(B)5號學生進入30秒跳繩決賽
(C)8號學生進入30秒跳繩決賽
(D)9號學生進入30秒跳繩決賽
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系xOy中,以原點為極點,x軸的正半軸為極軸建立極坐標系.已知曲線C:ρsin2θ=2acos θ(a>0),過點P(-2,-4)的直線l的參數(shù)方程為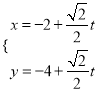 ,直線l與曲線C分別交于M,N兩點.若|PM|,|MN|,|PN|成等比數(shù)列,則a的值為________.
,直線l與曲線C分別交于M,N兩點.若|PM|,|MN|,|PN|成等比數(shù)列,則a的值為________.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com