
(本題14分)已知函數f (x) = ax3 +x2 -ax,其中a,x∈R.
(Ⅰ)若函數f (x)在區間(1,2)上不是單調函數,試求a的取值范圍;
(Ⅱ)直接寫出(不需給出運算過程)函數 的單調遞減區間;
的單調遞減區間;
(Ⅲ)如果存在a∈(-∞,-1],使得函數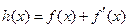 , x∈[-1, b](b > -1),在x = -1處取得最小值,試求b的最大值.
, x∈[-1, b](b > -1),在x = -1處取得最小值,試求b的最大值.
解:(Ⅰ)解法一: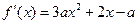
依題意知方程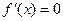 在區間(1,2)內有不重復的零點,
在區間(1,2)內有不重復的零點,
由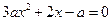 得
得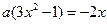
∵x∈(1,2), ∴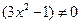
∴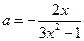 ;
;
令 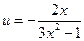 (x∈(1,2)),則
(x∈(1,2)),則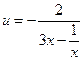 ,
,
∴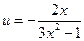 在區間(1,2)上是單調遞增函數,其值域為
在區間(1,2)上是單調遞增函數,其值域為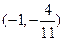 ,
,
故a的取值范圍是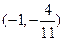 . ………………………5分
. ………………………5分
解法二: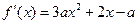
依題意知方程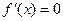 即
即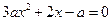 在區間(1,2)內有不重復的零點,
在區間(1,2)內有不重復的零點,
當a=0時,得 x=0,但0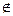 (1,2);
(1,2);
當a≠0時,方程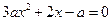 的△=1+12a2>0,
的△=1+12a2>0,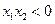 ,必有兩異號根,
,必有兩異號根,
欲使f (x)在區間(1,2)上不是 單調函數,方程
單調函數,方程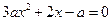 在(1,2)內一定有一根,設
在(1,2)內一定有一根,設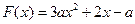 ,則F(1)·F(2)<0,
,則F(1)·F(2)<0,
即 (2a+2)(11a+4)<0,解得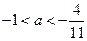 ,
,
故 a的取值范圍是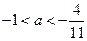 .
.
(解法二得分標準類比解法一)
(Ⅱ)函數g (x)的定義域為(0,+∞),
當 a≥0時,g (x)在(0,+∞)上單調遞增,無單調遞減區間;
當 a<0時,g (x)的單調遞減區間是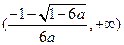 ………………8分
………………8分
(Ⅲ)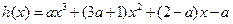 ;
;
依題意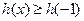 在區間[-1, b]上恒成立,
在區間[-1, b]上恒成立,
即 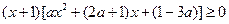 ①
①
當x∈[-1, b] 恒成立,
當 x=-1時,不等式①成立;
當 -1< x ≤b時,不等式①可化為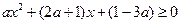 ②
②
令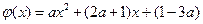 ,由a∈(-∞,-1]知,
,由a∈(-∞,-1]知,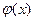 的圖像是
的圖像是
開口向下的拋物線,所以,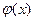 在閉區間上的最小值必在區間的端點處取得,
在閉區間上的最小值必在區間的端點處取得,
而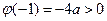 ,
,
∴不等式②恒成立的充要條件是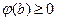 ,
,
即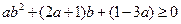 ,
,
亦即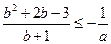 a∈(-∞,-1];
a∈(-∞,-1];
當a∈(-∞,-1]時,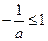 ,
,
∴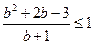 (b >-1), 即 b2+b-4 ≤ 0;
(b >-1), 即 b2+b-4 ≤ 0;
解得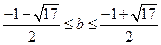 ;
;
但b >-1,∴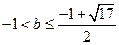 ;
;
故 b的最大值為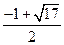 ,此時 a =-1符合題意. ……………14
,此時 a =-1符合題意. ……………14 分
分
解析


科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數f(x)=x3+ax2+bx+c在x=- 與x=1時都取得極值.
與x=1時都取得極值.
(1)求a、b的值與函數f(x)的單調區間;
(2)xÎ〔-1,2〕,不等式f(x)<c2恒成立,求c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(1 2分)若存在實數
2分)若存在實數 和
和 ,使得函數
,使得函數 與
與 對其定義域上的任意實數
對其定義域上的任意實數 分別滿足
分別滿足 :
: ,則稱直線
,則稱直線 為
為 與
與 的“和諧直線”.已知
的“和諧直線”.已知 為自然對數的底數);
為自然對數的底數);
(1)求 的極值;
的極值;
(2)函數 是否存在和諧直線?若存在,求出此和諧直線方程;若不存在,請說明理由.
是否存在和諧直線?若存在,求出此和諧直線方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數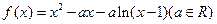 .
.
(1) 當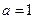 時,求函數
時,求函數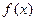 的最值;
的最值;
(2) 求函數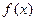 的單調區間;
的單調區間;
(3)(僅385班、389班學生做) 試說明是否存在實數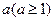 使
使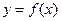 的圖象與
的圖象與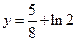 無公共點.
無公共點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com