【解析】A.設
，所以
是偶函數，所以選A.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案
目標測試系列答案科目：高中數學 來源： 題型：
（本小題滿分12分）
有編號為
,
,…
的10個零件，測量其直徑（單位：cm），得到下面數據：
其中直徑在區間[1.48，1.52]內的零件為一等品。
（Ⅰ）從上述10個零件中，隨機抽取一個，求這個零件為一等品的概率；
（Ⅱ）從一等品零件中，隨機抽取2個.
（ⅰ）用零件的編號列出所有可能的抽取結果；
（ⅱ）求這2個零件直徑相等的概率。本小題主要考查用列舉法計算隨機事件所含的基本事件數及事件發生的概率等基礎知識，考查數據處理能力及運用概率知識解決簡單的實際問題的能力。滿分12分
【解析】（Ⅰ）解：由所給數據可知，一等品零件共有6個.設“從10個零件中，隨機抽取一個為一等品”為事件A，則P（A）=
=
.
（Ⅱ）（i）解：一等品零件的編號為
.從這6個一等品零件中隨機抽取2個，所有可能的結果有：
,
,
,
,
,
,
共有15種.
(ii)解：“從一等品零件中，隨機抽取的2個零件直徑相等”（記為事件B）的所有可能結果有：
，
，共有6種.
所以P(B)=
.
（本小題滿分12分）
如圖，在五面體ABCDEF中，四邊形ADEF是正方形，FA⊥平面ABCD，BC∥AD，CD=1，AD=
，∠BAD＝∠CDA＝45°.
（Ⅰ）求異面直線CE與AF所成角的余弦值；
（Ⅱ）證明CD⊥平面ABF；
查看答案和解析>>
科目：高中數學 來源：2011-2012學年山東省高三下學期模擬預測理科數學試卷（解析版） 題型：解答題
在四棱錐
中，
平面
，底面為矩形，
.
（Ⅰ）當
時，求證：
；
（Ⅱ）若
邊上有且只有一個點
，使得
，求此時二面角
的余弦值.
【解析】第一位女利用線面垂直的判定定理和性質定理得到。當a=1時，底面ABCD為正方形，
又因為
,
………………2分
又
，得證。
第二問，建立空間直角坐標系，則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)……4分
設BQ=m，則Q(1，m,0)(0《m《a》
要使
，只要
所以
，即
………6分
由此可知時，存在點Q使得
當且僅當m=a-m，即m=a/2時，BC邊上有且只有一個點Q，使得
由此知道a=2, 設平面POQ的法向量為
,所以
平面PAD的法向量
則
的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
解：(Ⅰ)當時，底面ABCD為正方形，
又因為,又
………………3分
(Ⅱ) 因為AB,AD,AP兩兩垂直，分別以它們所在直線為X軸、Y軸、Z軸建立坐標系，如圖所示，
則B(1,0,1)D(0,a,0)C(1,a,0)P(0,0,1)…………4分
設BQ=m，則Q(1，m,0)(0《m《a》要使，只要
所以，即………6分
由此可知時，存在點Q使得
當且僅當m=a-m，即m=a/2時，BC邊上有且只有一個點Q，使得由此知道a=2,
設平面POQ的法向量為
,所以 平面PAD的法向量
則的大小與二面角A-PD-Q的大小相等所以
因此二面角A-PD-Q的余弦值為
查看答案和解析>>
科目：高中數學 來源：2011-2012學年山東省高三下學期模擬預測文科數學試卷（解析版） 題型：解答題
為了了解某市工人開展體育活動的情況，擬采用分層抽樣的方法從A，B，C三個區中抽取7個工廠進行調查，已知A，B，C區中分別有18，27，18個工廠
（Ⅰ）從A，B，C區中分別抽取的工廠個數；
（Ⅱ）若從抽取的7個工廠中隨機抽取2個進行調查結果的對比，計算這2個工廠中至少有1個來自A區的概率.
【解析】本試題主要考查了統計和概率的綜合運用。
第一問工廠總數為18+27+18=63，樣本容量與總體中的個體數比為7/63=1/9…3分
所以從A，B，C三個區中應分別抽取的工廠個數為2，3，2。
第二問設A1，A2為在A區中的抽得的2個工廠，B1，B2，B3為在B區中抽得的3個工廠，
C1，C2為在C區中抽得的2個工廠。
這7個工廠中隨機的抽取2個，全部的可能結果有1/2*7*6=32種。
隨機的抽取的2個工廠至少有一個來自A區的結果有A1，A2），A1，B2），A1，B1），
A1，B3）A1，C2），A1，C1）， …………9分
同理A2還能給合5種，一共有11種。
所以所求的概率為p=11/21
查看答案和解析>>
科目：高中數學 來源：2011-2012學年上海市崇明縣高三高考模擬考試二模理科數學試卷（解析版） 題型：解答題
如圖，已知四棱錐
的底面ABCD為正方形，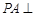
平面ABCD，E、F分別是BC，PC的中點，
，
．
（1）求證：
平面
；
（2）求二面角
的大小．
【解析】第一問利用線面垂直的判定定理和建立空間直角坐標系得到法向量來表示二面角的。
第二問中，以A為原點，如圖所示建立直角坐標系
，，
設平面FAE法向量為
，則
，
，
查看答案和解析>>
科目：高中數學 來源：2014屆山東省濟寧市高一下學期期中數學試卷（解析版） 題型：解答題
如圖所示，圓柱的高為2，底面半徑為
,AE、DF是圓柱的兩條母線，過
作圓柱的截面交下底面于
.
（1）求證：
；
（2）若四邊形ABCD是正方形，求證
；
（3）在（2）的條件下，求二面角A-BC-E的平面角的一個三角函數值。
【解析】第一問中，利用由圓柱的性質知：AD平行平面ＢＣＦＥ
又過作圓柱的截面交下底面于.
∥
又AE、DF是圓柱的兩條母線
∥ＤＦ，且ＡＥ＝ＤＦ 
ＡＤ∥ＥＦ
第二問中，由線面垂直得到線線垂直。四邊形ABCD是正方形
又
BC、AE是平面ABE內兩條相交直線
第三問中，設正方形ABCD的邊長為x,則在
在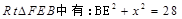
由（2）可知：
為二面角A-BC-E的平面角，所以
證明：（1）由圓柱的性質知：AD平行平面ＢＣＦＥ
又過作圓柱的截面交下底面于.∥
又AE、DF是圓柱的兩條母線
∥ＤＦ，且ＡＥ＝ＤＦ ＡＤ∥ＥＦ
(2)
四邊形ABCD是正方形 又
BC、AE是平面ABE內兩條相交直線
(3)設正方形ABCD的邊長為x,則在
在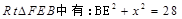
由（2）可知：為二面角A-BC-E的平面角，所以
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
外一點
分別作圓的切線和割線交圓于
,
，且
=7，
是圓上一點使得
=5，∠
=∠
, 則
= 。
