
 (江西卷理20文22)如圖,正三棱錐
(江西卷理20文22)如圖,正三棱錐![]() 的三條側棱
的三條側棱![]() 、
、![]() 、
、![]() 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 是
是![]() 的中點,過
的中點,過![]() 作平面與側棱
作平面與側棱![]() 、
、![]() 、
、![]() 或其延長線分別相交于
或其延長線分別相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1).求證:![]() ⊥平面
⊥平面![]() ;
;
(2).求二面角![]() 的大小;
的大小;
解 :(1)證明:依題設,![]() 是
是![]() 的中位線,所以
的中位線,所以![]() ∥
∥![]() ,
,
則![]() ∥平面
∥平面![]() ,所以
,所以![]() ∥
∥![]() 。
。
 又
又![]() 是
是![]() 的中點,所以
的中點,所以![]() ⊥
⊥![]() ,則
,則![]() ⊥
⊥![]() 。
。
因為![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]() ,
,
所以![]() ⊥面
⊥面![]() ,則
,則![]() ⊥
⊥![]() ,因此
,因此![]() ⊥面
⊥面![]() 。
。
(2)作![]() ⊥
⊥![]() 于
于![]() ,連
,連![]() 。因為
。因為![]() ⊥平面
⊥平面![]() ,
,
根據三垂線定理知,![]() ⊥
⊥![]() ,
,![]() 就是二面角
就是二面角![]() 的平面角。
的平面角。
作![]() ⊥
⊥![]() 于
于![]() ,則
,則![]() ∥
∥![]() ,則
,則![]() 是
是![]() 的中點,則
的中點,則![]() 。
。
設![]() ,由
,由![]() 得,
得,![]() ,解得
,解得![]() ,
,
在![]() 中,
中,![]() ,則,
,則,![]() 。
。
所以![]() ,故二面角
,故二面角![]() 為
為![]() 。
。
解法二:(1)以直線![]() 分別為
分別為![]() 軸,建立空間直角坐標系,
軸,建立空間直角坐標系,![]() 則
則![]()
所以![]()
所以![]() 所以
所以![]() 平面
平面![]()
由![]() ∥
∥![]() 得
得![]() ∥
∥![]() ,故:
,故:![]() 平面
平面![]()
(2)由已知![]() 設
設![]()
 則
則![]()
由![]() 與
與![]() 共線得:存在
共線得:存在![]() 有
有![]() 得
得
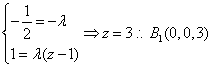
同理:![]()
![]()
設![]() 是平面
是平面![]() 的一個法向量,
的一個法向量,
則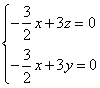 令
令![]() 得
得![]()
![]()
又![]() 是平面
是平面![]() 的一個法量
的一個法量
![]() 所以二面角的大小為
所以二面角的大小為![]()
(3)由(2)知,![]() ,
,![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]() 。
。
則![]() 。則點
。則點![]() 到平面
到平面![]() 的距離為
的距離為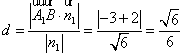


科目:高中數學 來源: 題型:
 (江西卷理20文22)如圖,正三棱錐
(江西卷理20文22)如圖,正三棱錐![]() 的三條側棱
的三條側棱![]() 、
、![]() 、
、![]() 兩兩垂直,且長度均為2.
兩兩垂直,且長度均為2.![]() 、
、![]() 分別是
分別是![]() 、
、![]() 的中點,
的中點,![]() 是
是![]() 的中點,過
的中點,過![]() 作平面與側棱
作平面與側棱![]() 、
、![]() 、
、![]() 或其延長線分別相交于
或其延長線分別相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1).求證:![]() ⊥平面
⊥平面![]() ;
;
(2).求二面角![]() 的大小;
的大小;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com