
(本小題14分)在奧運會射箭決賽中,參賽號碼為1~4號的四名射箭運動員參加射箭比賽。
(Ⅰ)通過抽簽將他們安排到1~4號靶位,試求恰有兩名運動員所抽靶位號與其參賽號碼相同的概率;
(Ⅱ)記1號、2號射箭運動員射箭的環數為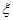 (
(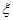 所有取值為0,1,2,3...,10)分別為
所有取值為0,1,2,3...,10)分別為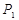 、
、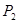 .根據教練員提供的資料,其概率分布如下表:
.根據教練員提供的資料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
|
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
① 若1,2號運動員各射箭一次,求兩人中至少有一人命中9環的概率;
② ②判斷1號,2號射箭運動員誰射箭的水平高?并說明理由.
(Ⅰ)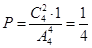
(Ⅱ)①p=1-0.476=0.524
②2號射箭運動員的射箭水平高.
【解析】本試題主要是考查了古典概型概率的運算,以及隨機變量的分布列的求解和期望值的運用。
(1)、4名運動員中任取兩名,其靶位號與參賽號相同,有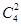 種方法,另2名運動員靶位號與參賽號均不相同的方法有1種,所以恰有一名運動員所抽靶位號與參賽號相同的概率為1/4
種方法,另2名運動員靶位號與參賽號均不相同的方法有1種,所以恰有一名運動員所抽靶位號與參賽號相同的概率為1/4
(2)由表可知,兩人各射擊一次,都未擊中9環的概率為P=(1-0.3)(1-0.32)=0.476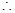 至少有一人命中9環的概率為p=1-0.476=0.524,那么利用各個取值概率值表示得到期望值,并比較大小得到水平高低問題。
至少有一人命中9環的概率為p=1-0.476=0.524,那么利用各個取值概率值表示得到期望值,并比較大小得到水平高低問題。
解(Ⅰ)從4名運動員中任取兩名,其靶位號與參賽號相同,有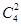 種方法,另2名運動員靶位號與參賽號均不相同的方法有1種,所以恰有一名運動員所抽靶位號與參賽號相同的概率為
種方法,另2名運動員靶位號與參賽號均不相同的方法有1種,所以恰有一名運動員所抽靶位號與參賽號相同的概率為 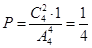
(Ⅱ)①由表可知,兩人各射擊一次,都未擊中9環的概率為P=(1-0.3)(1-0.32)=0.476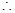 至少有一人命中9環的概率為p=1-0.476=0.524
至少有一人命中9環的概率為p=1-0.476=0.524
②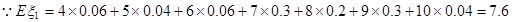
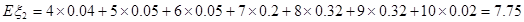
所以2號射箭運動員的射箭水平高.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2010年山東德州一中高一下學期模塊檢測數學卷 題型:解答題
(本小題14分)在平面直角坐標系中,O為坐標原點,已知向量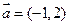 ,又有點
,又有點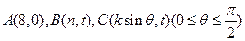
(1)若 ,且
,且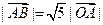 ,求向量
,求向量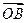 ;
;
(2)若向量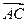 與向量
與向量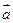 共線。當
共線。當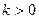 ,且函數
,且函數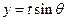 取最大值為4,求
取最大值為4,求 的值。
的值。
查看答案和解析>>
科目:高中數學 來源:2011年廣東省揭陽市第一中學高二上學期期末檢測數學文卷 題型:解答題
(本小題14分)在等比數列 中,
中, ,公比
,公比 ,且
,且 ,又
,又 與
與 的等比中項是2,
的等比中項是2,
(1)求數列 的通項公式;
的通項公式;
(2)設 ,數列
,數列 的前
的前 項和為
項和為 ,求
,求 .
.
查看答案和解析>>
科目:高中數學 來源:2010年山東德州一中高一下學期模塊檢測數學卷 題型:解答題
(本小題14分)在平面直角坐標系中,O為坐標原點,已知向量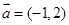 ,又有點
,又有點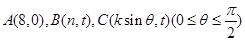
(1)若 ,且
,且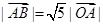 ,求向量
,求向量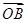 ;
;
(2)若向量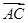 與向量
與向量 共線。當
共線。當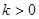 ,且函數
,且函數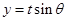 取最大值為4,求
取最大值為4,求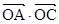 的值。
的值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com