
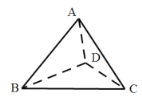
【題目】已知平面四邊形![]() 中,
中,![]() ,
,![]() ,再將
,再將![]() 沿著
沿著![]() 翻折成三棱錐
翻折成三棱錐![]() 的過程中,直線
的過程中,直線![]() 與平面
與平面![]() 所成角均小于直線
所成角均小于直線![]() 與平面
與平面![]() 所成角,設二面角
所成角,設二面角![]() ,
,![]() 的大小分別為
的大小分別為![]() ,則( )
,則( )
A.![]() B.
B.![]() C.存在
C.存在![]() D.存在
D.存在![]()
【答案】A
【解析】
根據條件在![]() 沿著
沿著![]() 翻折成三棱錐
翻折成三棱錐![]() 的過程中,直線
的過程中,直線![]() 與平面
與平面![]() 所成角均小于直線
所成角均小于直線![]() 與平面
與平面![]() 所成角,可得
所成角,可得![]() ,過點
,過點![]() 作
作![]()
![]() 平面
平面![]() ,為
,為![]() 垂足,過
垂足,過![]() 作
作![]()
![]()
![]() ,交
,交![]() 于點
于點![]() ,過
,過![]() 作
作![]()
![]()
![]() ,交
,交![]() 于點
于點![]() .連接
.連接![]() 根據
根據![]() ,
,![]() ,可得
,可得![]()
![]()
![]() ,且
,且![]() ,
,![]() ,所以有
,所以有![]() ,從而可得答案.
,從而可得答案.
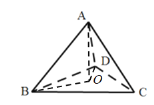
過點![]() 作
作![]()
![]() 平面
平面![]() ,為
,為![]() 垂足,連接
垂足,連接![]() .
.
則![]() 分別為直線
分別為直線![]() 與平面
與平面![]() 所成角和直線
所成角和直線![]() 與平面
與平面![]() 所成角.
所成角.
所以![]() .
.
又![]() 與平面
與平面![]() 所成角均小于直線
所成角均小于直線![]() 與平面
與平面![]() 所成角.
所成角.
所以![]() ,即
,即![]() .
.
平面四邊形![]() 中,
中,![]() ,則四點
,則四點![]() 共圓.
共圓.
![]() ,設
,設![]() 的垂直平分線為
的垂直平分線為![]() ,將
,將![]() 沿著
沿著![]() 折起.
折起.
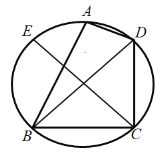
![]() 為該圓的一條直徑,由
為該圓的一條直徑,由![]() ,所以點
,所以點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在半圓
在半圓![]() 內,如圖.
內,如圖.
所以點![]() 到直線
到直線![]() 的距離大于到直線
的距離大于到直線![]() 的距離.
的距離.
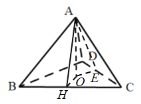
過![]() 作
作![]()
![]()
![]() ,交
,交![]() 于點
于點![]() ,過
,過![]() 作
作![]()
![]()
![]() ,交
,交![]() 于點
于點![]() .連接
.連接![]() ,如圖
,如圖
則![]()
![]()
![]() ,
,
由![]() 平面
平面![]() ,所以
,所以![]()
![]()
![]() ,又
,又![]()
![]()
![]() ,所以
,所以![]()
![]() 平面
平面![]() .
.
所以![]()
![]()
![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,即
的平面角,即![]() .
.
同理可得:![]() .由
.由![]() 在半圓
在半圓![]() 內,則
內,則![]() 為銳角.
為銳角.
![]() ,則
,則![]()
所以![]()
故選:A.


 世紀百通期末金卷系列答案
世紀百通期末金卷系列答案科目:高中數學 來源: 題型:
【題目】為了解廣大學生家長對校園食品安全的認識,某市食品安全檢測部門對該市家長進行了一次校園食品安全網絡知識問卷調查,每一位學生家長僅有一次參加機會,現對有效問卷進行整理,并隨機抽取出了200份答卷,統計這些答卷的得分(滿分:100分)制出的頻率分布直方圖如圖所示,由頻率分布直方圖可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,其中
,其中![]() 近似為這200人得分的平均值(同一組數據用該組區間的中點值作為代表).
近似為這200人得分的平均值(同一組數據用該組區間的中點值作為代表).
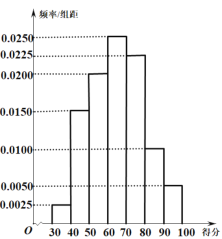
(1)請利用正態分布的知識求![]() ;
;
(2)該市食品安全檢測部門為此次參加問卷調查的學生家長制定如下獎勵方案:
①得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費:
的可以獲贈1次隨機話費:
②每次獲贈的隨機話費和對應的概率為:
獲贈的隨機話費(單位:元) |
|
|
概率 |
|
|
市食品安全檢測部門預計參加此次活動的家長約5000人,請依據以上數據估計此次活動可能贈送出多少話費?
附:①![]() ;②若
;②若![]() ;則
;則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() ax﹣lnx(a∈R).
ax﹣lnx(a∈R).
(1)若a=2時,求函數f(x)的單調區間;
(2)設g(x)=f(x)![]() 1,若函數g(x)在
1,若函數g(x)在![]() 上有兩個零點,求實數a的取值范圍.
上有兩個零點,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 。
。
(Ⅰ)如果存在x1,x2∈[0,2],使得g(x1)-g(x2)≥M成立,求滿足上述條件的最大整數M;
(Ⅱ)如果對于任意的![]() 都有f(s)≥g(t)成立,求實數a的取值范圍.
都有f(s)≥g(t)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 九章算術
九章算術![]() 中有一題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬,”馬主曰:“我馬食半牛”,今欲衰償之,問各出幾何?其意:今有牛、馬、羊吃了別人的禾苗,苗主人要求賠償五斗粟,羊主人說:“我羊所吃的禾苗只有馬的一半”馬主人說:“我馬所吃的禾苗只有牛的一半”打算按此比例償還,問羊的主人應賠償______斗粟,在這個問題中牛主人比羊主人多賠償______斗粟.
中有一題:今有牛、馬、羊食人苗,苗主責之粟五斗,羊主曰:“我羊食半馬,”馬主曰:“我馬食半牛”,今欲衰償之,問各出幾何?其意:今有牛、馬、羊吃了別人的禾苗,苗主人要求賠償五斗粟,羊主人說:“我羊所吃的禾苗只有馬的一半”馬主人說:“我馬所吃的禾苗只有牛的一半”打算按此比例償還,問羊的主人應賠償______斗粟,在這個問題中牛主人比羊主人多賠償______斗粟.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接2019年全國文明城市評比,某市文明辦對市民進行了一次文明創建知識的網絡問卷調查.每一位市民有且僅有一次參加機會,通過隨機抽樣,得到參加問卷調查的1000人的得分(滿分:100分)數據,統計結果如下表所示:
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由頻數分布表可以認為,此次問卷調查的得分![]() 服從正態分布
服從正態分布![]() ,
,![]() 近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求
近似為這1000人得分的平均值(同一組數據用該組區間的中點值作為代表),請利用正態分布的知識求![]() ;
;
(2)在(1)的條件下,文明辦為此次參加問卷調查的市民制定如下獎勵方案:
(i)得分不低于![]() 的可以獲贈2次隨機話費,得分低于
的可以獲贈2次隨機話費,得分低于![]() 的可以獲贈1次隨機話費;
的可以獲贈1次隨機話費;
(ii)每次獲贈的隨機話費和對應的概率為:
獲贈的隨機話費(單位:元) | 20 | 40 |
概率 |
|
|
現市民小王要參加此次問卷調查,記![]() (單位:元)為該市民參加問卷調查獲贈的話費,求
(單位:元)為該市民參加問卷調查獲贈的話費,求![]() 的分布列及數學期望.
的分布列及數學期望.
附:①![]() ;
;
②若![]() ,則
,則![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() ,
,![]() ,
,![]() 分別為橢圓的右頂點,上頂點和右焦點,且
分別為橢圓的右頂點,上頂點和右焦點,且![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)![]() ,
,![]() 是橢圓上的兩個動點,若直線
是橢圓上的兩個動點,若直線![]() 與直線
與直線![]() 的斜率之和為
的斜率之和為![]() ,證明,直線
,證明,直線![]() 恒過定點.
恒過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com