
(本小題滿分14分)已知定義域為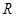 的單調(diào)函數(shù)
的單調(diào)函數(shù)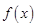 是奇函數(shù),當
是奇函數(shù),當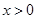 時,
時, .
.
(I)求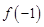 的值;
的值;
(II)求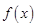 的解析式;
的解析式;
(III)若對任意的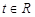 ,不等式
,不等式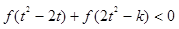 恒成立,求實數(shù)
恒成立,求實數(shù)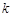 的取值范圍.
的取值范圍.
(1)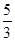 ;(2)
;(2)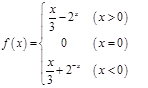 ;(3)
;(3)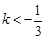 。
。
解析試題分析: (I)因為f(x)是奇函數(shù),所以f(-1)=-f(1)從而問題得解.
(II)因為f(x)為R上的奇函數(shù),所以f(0)=0,然后用-x代替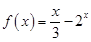 中的x,-f(x)代替
中的x,-f(x)代替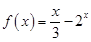 中的f(x)再兩邊同乘以-1可得x<0的解析式.從而可得f(x)在R上的解析式是一個分段函數(shù).
中的f(x)再兩邊同乘以-1可得x<0的解析式.從而可得f(x)在R上的解析式是一個分段函數(shù).
(III) 因為f(x)為定義域為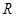 的單調(diào)函數(shù),并且由于由于當x
的單調(diào)函數(shù),并且由于由于當x
>0時,f(x)是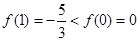 ,從而可得f(x)在R上是減函數(shù),所以由
,從而可得f(x)在R上是減函數(shù),所以由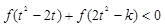 得
得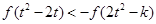 進一步可得
進一步可得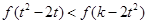 ,所以
,所以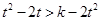 ,然后再轉(zhuǎn)化為一元二次不等式恒成立問題解決即可。
,然后再轉(zhuǎn)化為一元二次不等式恒成立問題解決即可。
(1)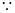 定義域為
定義域為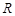 的函數(shù)
的函數(shù)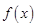 是奇函數(shù) ,所以
是奇函數(shù) ,所以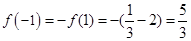 -------2分
-------2分
(2)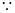 定義域為
定義域為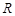 的函數(shù)
的函數(shù)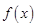 是奇函數(shù)
是奇函數(shù) 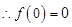 ------------4分
------------4分
當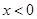 時,
時,
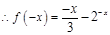
又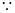 函數(shù)
函數(shù)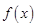 是奇函數(shù)
是奇函數(shù) 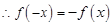
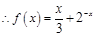 ------------7分
------------7分
綜上所述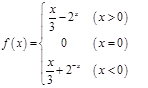 ----8分
----8分
(3)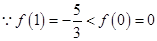 且
且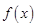 在
在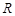 上單調(diào)
上單調(diào)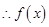 在
在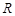 上單調(diào)遞減 -------10分
上單調(diào)遞減 -------10分
由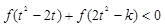 得
得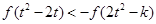
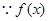 是奇函數(shù)
是奇函數(shù) 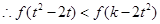
,又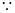
 是減函數(shù)
是減函數(shù) 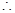
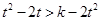 ------------12分
------------12分
即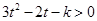 對任意
對任意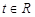 恒成立
恒成立 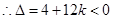 得
得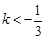 即為所求----------------14分
即為所求----------------14分
考點:函數(shù)的奇偶性,單調(diào)性,以及利用函數(shù)的單調(diào)性解不等式.
點評:奇函數(shù)的圖像關(guān)于原點對稱,因而在求對稱區(qū)間上的解析式時,可用利用-x,-f(x)分別代替對稱區(qū)間上解析式中的x,f(x)即可得到所求區(qū)間上的解析式.另外奇函數(shù)在對稱區(qū)間上具有相同的單調(diào)性,當定義域中有0值時,f(0)=0這些都是奇函數(shù)常用的結(jié)論,勿必記住.


科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分14分)已知函數(shù)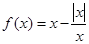 .
.
(1)作出函數(shù) 的圖象;
的圖象;
(2)寫出函數(shù) 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(3)判斷函數(shù) 的奇偶性,并用定義證明.
的奇偶性,并用定義證明.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分14分)
已知函數(shù) .
.
(1)求證:函數(shù) 在
在 上是單調(diào)遞增函數(shù);
上是單調(diào)遞增函數(shù);
(2)當 時,求函數(shù)在
時,求函數(shù)在 上的最值;
上的最值;
(3)函數(shù) 在
在 上恒有
上恒有 成立,求
成立,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)已知函數(shù) 為奇函數(shù);
為奇函數(shù);
(1)求 以及m的值;
以及m的值;
(2)在給出的直角坐標系中畫出 的圖象;
的圖象;
(3)若函數(shù) 有三個零點,求實數(shù)k的取值范圍.
有三個零點,求實數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知平面上的線段l及點P,在l上任取一點Q,線段PQ長度的最小值稱為點P到線段l的距離,記作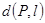 。
。
(1)已知點 ,線段
,線段 ,求
,求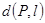 ;
;
(2)設(shè)A(-1,0),B(1,0),求點集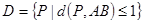 所表示圖形的面積;
所表示圖形的面積;
(3)若M(0,1),O(0,0),N(2,0),畫出集合 所表示的圖形。(本題滿分14分)
所表示的圖形。(本題滿分14分)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)函數(shù) 是R上的偶函數(shù),且當
是R上的偶函數(shù),且當 時,函數(shù)解析式為
時,函數(shù)解析式為 ,
,
(Ⅰ)求 的值;
的值;
(Ⅱ)求當 時,函數(shù)的解析式。
時,函數(shù)的解析式。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) 的定義域為
的定義域為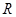 ,對于任意的
,對于任意的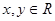 ,都有
,都有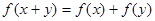 ,且當
,且當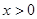 時,
時,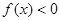 ,若
,若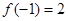 .
.
(1)求證: 為奇函數(shù);
為奇函數(shù);
(2)求證: 是
是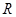 上的減函數(shù);
上的減函數(shù);
(3)求函數(shù) 在區(qū)間
在區(qū)間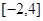 上的值域.
上的值域.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分13分)
已知函數(shù)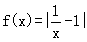
(Ⅰ)判斷f(x)在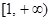 上的單調(diào)性,并證明你的結(jié)論;
上的單調(diào)性,并證明你的結(jié)論;
(Ⅱ)若集合A="{y" | y=f(x), },B=[0,1], 試判斷A與B的關(guān)系;
},B=[0,1], 試判斷A與B的關(guān)系;
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com