
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1,-e2),求證:A、B、D三點共線;
=3(e1,-e2),求證:A、B、D三點共線;
(2)試確定實數k,使ke1+e2和e1+ke2共線.
思路分析:本題主要考查向量基本定理和向量共線的條件.(1)可以將e1,e2看作一組基底表示我們需要的向量,如![]() ,
,![]() =
=![]() +
+![]() =2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共線條件進行證明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出來的兩個向量,既然兩向量共線,就可以用共線條件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
=2e1+8e2+3e1-3e2=5e1+5e2然后利用向量共線條件進行證明.(2)由于向量ke1+e2,e1+ke2都是用基底e1,e2表示出來的兩個向量,既然兩向量共線,就可以用共線條件得到(ke1+e2)=λ(e1+ke2),解出k值即可.
(1)證明:∵![]() =e1+e2,
=e1+e2,
![]() +
+![]()
=2e1+8e2+3e1-3e2
=5(e1+e2)=5![]() ,
,
∴![]() 、BD共線.又有公共點B,∴A、B、D三點共線.
、BD共線.又有公共點B,∴A、B、D三點共線.
(2)解:∵ke1+e2與e1+ke2共線,
∴存在λ使ke1+e2=λ(e1+ke2),
則(k-λ)e1=(λk-1)e2.由于e1與e2不共線,
∴只能有![]() 則k=±1.
則k=±1.
溫馨提示
題目中已給出一組基底e1,e2,則該平面中任一向量都可以與之建立聯(lián)系,以該基底為紐帶,可以溝通不同向量之間的聯(lián)系.本題要證三點共線,由這三點中任意兩點確定兩個向量.然后用基底e1,e2表示,并依據向量共線的條件來證明這兩個向量共線.又這兩個向量有公共點,于是證三點共線.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案科目:高中數學 來源: 題型:
| AB |
| BC |
| CD |
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學必修4 2.5向量的應用練習卷(解析版) 題型:解答題
設兩非零向量e1和e2不共線.
(1)如果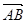 =
= +
+  ,
,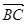 =2
=2  +8
+8  ,
,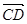 =3(
=3( -
- ),求證:A、B、D三點共線;
),求證:A、B、D三點共線;
(2)試確定實數k,使k  +
+  和
和 +k
+k  共線;
共線;
(3)若|  |=2,|
|=2,|  |=3,
|=3,  與
與 的夾角為60°,試確定k的值,使k
的夾角為60°,試確定k的值,使k  +
+  與
與 +k
+k  垂直.
垂直.
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)如果![]() =e1+e2,
=e1+e2,![]() =2e1+8e2,
=2e1+8e2,![]() =3(e1-e2),求證:A、B、D三點共線;
=3(e1-e2),求證:A、B、D三點共線;
(2)試確定實數k,使ke1+e2和e1+ke2共線.
查看答案和解析>>
科目:高中數學 來源:《2.4-2.5 平面向量的數量積及平面向量的應用舉例》2011年同步練習(解析版) 題型:解答題
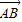 =e1+e2,
=e1+e2,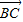 =2e1+8e2,
=2e1+8e2,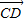 =3(e1-e2),求證:A、B、D三點共線;
=3(e1-e2),求證:A、B、D三點共線;查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com