
對于函數![]() ,若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點.如果函數f(x)=
,若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點.如果函數f(x)=![]() 有且僅有兩個不動點0和2.
有且僅有兩個不動點0和2.
(Ⅰ)試求b、c滿足的關系式;
(Ⅱ)若c=2時,各項不為零的數列{an}滿足4Sn?f(![]() )=1,求證:
)=1,求證:![]() <
<![]() <
<![]() ;
;
(Ⅲ)設bn=-![]() ,Tn為數列{bn}的前n項和,求證:T2009-1<ln2009<T2008.
,Tn為數列{bn}的前n項和,求證:T2009-1<ln2009<T2008.
解析:(Ⅰ)設![]()
∴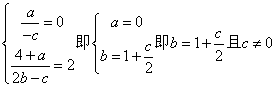 ………………………………2分
………………………………2分
(Ⅱ)∵c=2 ∴b=2 ∴![]() ,
,
由已知可得2Sn=an-an2……①,且an≠1.
當n≥2時,2 Sn -1=an-1-an-12 ……②,
①-②得(an+an-1)( an-an-1+1)=0,∴an=-an-1 或 an=-an-1 =-1,
當n=1時,2a1=a1-a12 ![]() a1=-1,
a1=-1,
若an=-an-1,則a2=1與an≠1矛盾.∴an-an-1=-1, ∴an=-n.………………4分
∴要證待證不等式,只要證 ![]() ,
,
即證 ![]() ,
,
只要證 ![]() ,即證
,即證 ![]() .
.
考慮證不等式![]() (x>0) **.…………………………………………………6分
(x>0) **.…………………………………………………6分
令g(x)=x-ln(1+x), h(x)=ln(x+1)-![]() (x>0) .
(x>0) .
∴g '(x)=![]() , h '(x)=
, h '(x)=![]() ,
,
∵x>0, ∴g '(x)>0, h '(x)>0,∴g(x)、h(x)在(0, +∞)上都是增函數,
∴g(x)>g(0)=0, h(x)>h(0)=0,∴x>0時,![]() .
.
令![]() 則**式成立,∴
則**式成立,∴![]() <
<![]() <
<![]() ,……………………………………9分
,……………………………………9分
(Ⅲ)由(Ⅱ)知bn=![]() ,則Tn=
,則Tn=![]() .
.
在![]() 中,令n=1,2,3,……,2008,并將各式相加,
中,令n=1,2,3,……,2008,并將各式相加,
得![]() ,
,
即T2009-1<ln2009<T2008.…………………………………………………………………12分


科目:高中數學 來源: 題型:
對于函數![]() ,若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點.如果函數f(x)=
,若存在x0∈R,使f(x0)=x0成立,則稱x0為f(x)的不動點.如果函數f(x)=![]() 有且僅有兩個不動點0和2.
有且僅有兩個不動點0和2.
(Ⅰ)試求b、c滿足的關系式;
(Ⅱ)若c=2時,各項不為零的數列{an}滿足4Sn·f(![]() )=1,
)=1,
求證:![]() <
<![]() <
<![]() ;
;
(Ⅲ)設bn=-![]() ,Tn為數列{bn}的前n項和,求證:T2009-1<ln2009<T2008.
,Tn為數列{bn}的前n項和,求證:T2009-1<ln2009<T2008.
查看答案和解析>>
科目:高中數學 來源:2015屆福建省高一上學期期中考試數學試卷(解析版) 題型:解答題
對于函數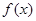 ,若存在x0∈R,使方程
,若存在x0∈R,使方程 成立,則稱x0為
成立,則稱x0為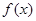 的不動點,已知函數
的不動點,已知函數 (a≠0).
(a≠0).
(1)當 時,求函數
時,求函數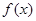 的不動點;
的不動點;
(2)若對任意實數b,函數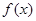 恒有兩個相異的不動點,求a的取值范圍;
恒有兩個相異的不動點,求a的取值范圍;
查看答案和解析>>
科目:高中數學 來源:2010年福建省高一上學期期中考試數學卷 題型:解答題
(本小題滿10分)注意:第(3)小題平行班學生不必做,特保班學生必須做。對于函數 ,若存在x0∈R,使
,若存在x0∈R,使 成立,則稱x0為
成立,則稱x0為 的不動點。已知函數
的不動點。已知函數 (a≠0)。
(a≠0)。
(1)當 時,求函數
時,求函數 的不動點;
的不動點;
(2)若對任意實數b,函數 恒有兩個相異的不動點,求a的取值范圍;
恒有兩個相異的不動點,求a的取值范圍;
(3)(特保班做) 在(2)的條件下,若 圖象上A、B兩點的橫坐標是函數
圖象上A、B兩點的橫坐標是函數 的不動點,且A、B兩點關于點
的不動點,且A、B兩點關于點 對稱,求
對稱,求 的的最小值。
的的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿10分)注意:第(3)小題平行班學生不必做,特保班學生必須做。
對于函數![]() ,若存在x0∈R,使
,若存在x0∈R,使![]() 成立,則稱x0為
成立,則稱x0為![]() 的不動點。
的不動點。
已知函數![]() (a≠0)。
(a≠0)。
(1)當![]() 時,求函數
時,求函數![]() 的不動點;
的不動點;
(2)若對任意實數b,函數![]() 恒有兩個相異的不動點,求a的取值范圍;
恒有兩個相異的不動點,求a的取值范圍;
(3)(特保班做) 在(2)的條件下,若![]() 圖象上A、B兩點的橫坐標是函數
圖象上A、B兩點的橫坐標是函數![]() 的不動點,且A、B兩點關于點
的不動點,且A、B兩點關于點![]() 對稱,求
對稱,求![]() 的的最小值。
的的最小值。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com