
(本小題滿分10分)如圖,四邊形ABCD是正方形,O是正方形的中心,PO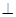 底面ABCD,E是PC的中點.
底面ABCD,E是PC的中點.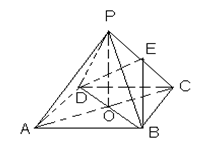
求證:(1) PA∥平面BDE .
(2)平面PAC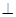 平面BDE .
平面BDE .
(1)根據題意,由于O是AC的中點,E是PC的中點,
所以OE∥AP,可知結合線面平行的判定定理得到證明。
(2)根據已知條件可知因為PO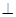 底面ABCD,BD
底面ABCD,BD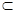 平面BDE,
平面BDE,
所以PO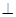 BD,再結合BD
BD,再結合BD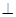 平面PAC,進而得到證明。
平面PAC,進而得到證明。
解析試題分析:證明
(1)連接O、E兩點. 1分
因為O是AC的中點,E是PC的中點,
所以OE∥AP, 3分
又因為OE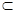 平面BDE,PA
平面BDE,PA 平面BDE,
平面BDE,
所以PA∥平面BDE 5分
(2)因為PO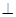 底面ABCD,BD
底面ABCD,BD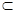 平面BDE,
平面BDE,
所以PO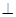 BD, 6分
BD, 6分
又因為四邊形ABCD是正方形,AC與BD是對角線
所以 AC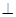 BD,且AC
BD,且AC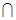 PO=O 7分
PO=O 7分
所以BD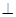 平面PAC, 8分
平面PAC, 8分
因為BD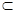 平面BDE,
平面BDE,
所以平面PAC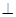 平面BDE. 0分
平面BDE. 0分
考點:空間中點線面的位置關系的運用。
點評:解決該試題的關鍵是利用線面的平行和垂直的判定定理來分析加以證明,考查了空間想像力。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
如圖,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,點E、F分別在棱BB1、CC1上,且BE=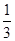 BB1,C1F=
BB1,C1F=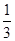 CC1.
CC1.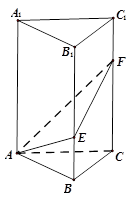
(1)求異面直線AE與A1 F所成角的大小;
(2)求平面AEF與平面ABC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知四棱錐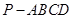 中
中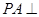 平面
平面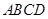 ,
,
且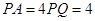 ,底面為直角梯形,
,底面為直角梯形,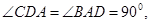
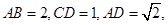
 分別是
分別是 的中點.
的中點.
(1)求證: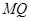 // 平面
// 平面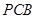 ;
;
(2)求截面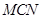 與底面
與底面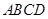 所成二面角的大小;
所成二面角的大小;
(3)求點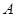 到平面
到平面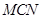 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖:在底面為直角梯形的四棱錐P-ABCD中,AD‖BC ,∠ABC=90°,PA⊥平面ABCD, PA="3," AD="2," AB=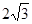 , BC=6.
, BC=6.
(1)求證:BD⊥平面PAC
(2)求二面角B-PC-A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知兩個正四棱錐P-ABCD與Q-ABCD的高分別為1和2,AB=4.
(Ⅰ)證明PQ⊥平面ABCD;
(Ⅱ)求異面直線AQ與PB所成的角;
(Ⅲ)求點P到平面QAD的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)如圖所示,四棱錐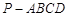 中,底面
中,底面 是邊長為2的菱形,
是邊長為2的菱形,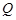 是棱
是棱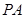 上的動點.
上的動點.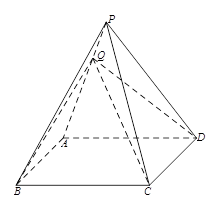
(Ⅰ)若 是
是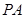 的中點,求證:
的中點,求證: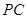 //平面
//平面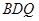 ;
;
(Ⅱ)若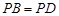 ,求證:
,求證: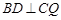 ;
;
(III)在(Ⅱ)的條件下,若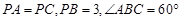 ,求四棱錐
,求四棱錐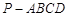 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,直四棱柱ABCD—A1B1C1D1的高為3,底面是邊長為4且∠DAB=60°的菱形,AC∩BD=0,A1C1∩B1D1=O1,E是O1A的中點.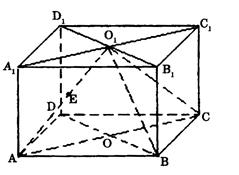
(1)求證:平面O1AC 平面O1BD
平面O1BD
(2)求二面角O1-BC-D的大小;
(3)求點E到平面O1BC的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com