
【題目】已知命題p:x∈[-1,2],函數(shù)f(x)=x2-x的值大于0,若p∨q是真命題,則命題q可以是( )
A. x0∈(-1,1),cos x0<![]()
B. “-3<m<0”是“函數(shù)f(x)=x+log2x+m在區(qū)間![]() 上有零點(diǎn)”的必要不充分條件
上有零點(diǎn)”的必要不充分條件
C. x=![]() 是曲線f(x)=
是曲線f(x)=![]() sin 2x+cos 2x的一條對(duì)稱軸
sin 2x+cos 2x的一條對(duì)稱軸
D. 若x∈(0,2),則在曲線f(x)=ex(x-2)上任意一點(diǎn)處的切線的斜率不小于![]()
【答案】C
【解析】
由題意易知p是假命題,故只需q是真命題,逐一判斷選項(xiàng)即可解決.
對(duì)于命題p:函數(shù)f(x)=x2-x=![]() ,則函數(shù)f(x)在
,則函數(shù)f(x)在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增.∴當(dāng)x=
上單調(diào)遞增.∴當(dāng)x=![]() 時(shí),f(x)取得最小值,
時(shí),f(x)取得最小值,![]() ,因此命題p是假命題.若p∨q是真命題,則命題q必須是真命題.A中,x∈(-1,1),cos x∈(cos 1,1],而cos 1>
,因此命題p是假命題.若p∨q是真命題,則命題q必須是真命題.A中,x∈(-1,1),cos x∈(cos 1,1],而cos 1>![]() ,因此A是假命題;B中,函數(shù)f(x)=x+log2x+m在區(qū)間
,因此A是假命題;B中,函數(shù)f(x)=x+log2x+m在區(qū)間![]() 上單調(diào)遞增,若函數(shù)f(x)在此區(qū)間上有零點(diǎn),則
上單調(diào)遞增,若函數(shù)f(x)在此區(qū)間上有零點(diǎn),則![]() ,解得
,解得![]() ,因此“-3<m<0”是“函數(shù)f(x)=x+log2x+m在區(qū)間
,因此“-3<m<0”是“函數(shù)f(x)=x+log2x+m在區(qū)間![]() 上有零點(diǎn)”的充分不必要條件,因此B是假命題;C中,f(x)=
上有零點(diǎn)”的充分不必要條件,因此B是假命題;C中,f(x)=![]() sin 2x+cos 2x=
sin 2x+cos 2x=![]() ,當(dāng)x=
,當(dāng)x=![]() 時(shí),
時(shí),![]() ,因此x=
,因此x=![]() 是曲線y=f(x)的一條對(duì)稱軸,C是真命題;D中,f(x)=ex(x-2),f′(x)=ex+ex(x-2)=ex(x-1),當(dāng)x∈(0,2)時(shí),f′(x)>f′(0)=-1,因此D是假命題.
是曲線y=f(x)的一條對(duì)稱軸,C是真命題;D中,f(x)=ex(x-2),f′(x)=ex+ex(x-2)=ex(x-1),當(dāng)x∈(0,2)時(shí),f′(x)>f′(0)=-1,因此D是假命題.


 教學(xué)練新同步練習(xí)系列答案
教學(xué)練新同步練習(xí)系列答案 課前課后同步練習(xí)系列答案
課前課后同步練習(xí)系列答案 課堂小作業(yè)系列答案
課堂小作業(yè)系列答案 黃岡小狀元口算速算練習(xí)冊(cè)系列答案
黃岡小狀元口算速算練習(xí)冊(cè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,已知橢圓 ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,長(zhǎng)軸長(zhǎng)為4,過(guò)橢圓的左頂點(diǎn)A作直線l,分別交橢圓和圓x2+y2=a2于相異兩點(diǎn)P,Q.
,長(zhǎng)軸長(zhǎng)為4,過(guò)橢圓的左頂點(diǎn)A作直線l,分別交橢圓和圓x2+y2=a2于相異兩點(diǎn)P,Q. 
(1)若直線l的斜率為 ![]() ,求
,求 ![]() 的值;
的值;
(2)若 ![]() =λ
=λ ![]() ,求實(shí)數(shù)λ的取值范圍.
,求實(shí)數(shù)λ的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某公園準(zhǔn)備在一圓形水池里設(shè)置兩個(gè)觀景噴泉,觀景噴泉的示意圖如圖所示,A,B兩點(diǎn)為噴泉,圓心O為AB的中點(diǎn),其中OA=OB=a米,半徑OC=10米,市民可位于水池邊緣任意一點(diǎn)C處觀賞. 
(1)若當(dāng)∠OBC= ![]() 時(shí),sin∠BCO=
時(shí),sin∠BCO= ![]() ,求此時(shí)a的值;
,求此時(shí)a的值;
(2)設(shè)y=CA2+CB2 , 且CA2+CB2≤232.
(i)試將y表示為a的函數(shù),并求出a的取值范圍;
(ii)若同時(shí)要求市民在水池邊緣任意一點(diǎn)C處觀賞噴泉時(shí),觀賞角度∠ACB的最大值不小于 ![]() ,試求A,B兩處噴泉間距離的最小值.
,試求A,B兩處噴泉間距離的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,底面![]() 是邊長(zhǎng)為3的正方形,
是邊長(zhǎng)為3的正方形,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() .
.

(1)求證:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知曲線C的極坐標(biāo)方程是ρ=2sinθ,直線l的參數(shù)方程是  (t為參數(shù)).設(shè)直線l與x軸的交點(diǎn)是M,N是曲線C上一動(dòng)點(diǎn),求MN的最大值.
(t為參數(shù)).設(shè)直線l與x軸的交點(diǎn)是M,N是曲線C上一動(dòng)點(diǎn),求MN的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,以原點(diǎn)O為頂點(diǎn),以y軸為對(duì)稱軸的拋物線E的焦點(diǎn)為F(0,1),點(diǎn)M是直線l:y=m(m<0)上任意一點(diǎn),過(guò)點(diǎn)M引拋物線E的兩條切線分別交x軸于點(diǎn)S,T,切點(diǎn)分別為B,A.
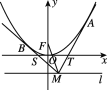
(1)求拋物線E的方程;
(2)求證:點(diǎn)S,T在以FM為直徑的圓上.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的四棱錐P﹣ABCD中,四邊形ABCD為正方形,PA⊥CD,BC⊥平面PAB,且E,M,N分別為PD,CD,AD的中點(diǎn), ![]() =3
=3 ![]() .
. 
(1)證明:PB∥平面FMN;
(2)若PA=AB,求二面角E﹣AC﹣B的余弦值. 
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,橢圓 ![]() =1(a>b>0)的左、右頂點(diǎn)分別為A,B,焦距為2
=1(a>b>0)的左、右頂點(diǎn)分別為A,B,焦距為2 ![]() ,直線x=﹣a與y=b交于點(diǎn)D,且|BD|=3
,直線x=﹣a與y=b交于點(diǎn)D,且|BD|=3 ![]() ,過(guò)點(diǎn)B作直線l交直線x=﹣a于點(diǎn)M,交橢圓于另一點(diǎn)P.
,過(guò)點(diǎn)B作直線l交直線x=﹣a于點(diǎn)M,交橢圓于另一點(diǎn)P. 
(1)求橢圓的方程;
(2)證明: ![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是一次考試成績(jī)的樣本頻率分布直方圖(樣本容量n=200),若成績(jī)不低于60分為及格,則樣本中的及格人數(shù)是( )

A. 6 B. 36 C. 60 D. 120
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com