
【題目】頂點在原點,焦點在x軸正半軸的拋物線,經過點(3,6),
(1)求拋物線截直線y=2x﹣6所得的弦長.
(2)討論直線y=kx+1與拋物線的位置關系,并求出相應的k的取值范圍.
【答案】
(1)
解:由題意可知:設拋物線的方程為:y2=2px,(p>0),
由拋物線經過點(3,6),
∴36=2×p×3,解得:p=6,
∴拋物線方程為:y2=12x,
設直線y=2x﹣6與拋物線兩交點A(x1,y1),B(x2,y2),
由 ![]() ,整理得:x2﹣9x+9=0,
,整理得:x2﹣9x+9=0,
由韋達定理可知:x1+x2=9,x1x2=9,
∴|AB|= ![]()
![]() =
= ![]()
![]() =15,
=15,
拋物線截直線y=2x﹣6所得的弦長15
(2)
解:當k=0時,y=1,直線與拋物線有一個交點,
當k≠0時,由 ![]() ,整理得:k2x2+2(k﹣6)x+1=0,
,整理得:k2x2+2(k﹣6)x+1=0,
當△=4(k﹣6)2﹣4k2>0,解得:k<3,
∴直線與拋物線有兩個交點,
△=4(k﹣6)2﹣4k2<0,解得:k>3,
直線與拋物線無交點,
當△=4(k﹣6)2﹣4k2=0,即k=3時,
直線與拋物線有一個交點,
綜上可知:當k>3時,直線y=kx+1與拋物線相離,即直線與拋物線無交點,
當k=3時,直線y=kx+1與拋物線相切,直線與拋物線有一個交點,
當k<3且k≠0,直線與拋物線相交,有兩個交點,
當k=0時,直線與拋物線相交,有一個交點
【解析】(1)由題意設橢圓的方程為:y2=2px,(p>0),由拋物線經過點(3,6),代入即可求得p的值,求得拋物線方程,將y=2x﹣6代入y2=12x,由韋達定理求得x1+x2=9,x1x2=9,根據弦長公式可知:|AB|= ![]()
![]() ,即可求得拋物線截直線y=2x﹣6所得的弦長;(2)當k=0時,y=1,直線與拋物線有一個交點,當k≠0時,將y=kx+1代入拋物線方程,由△>0,直線與拋物線有兩個交點,求得k的取值范圍,當△<0,直線與拋物線相離,無交點,求得k的取值范圍,當△=0,直線與拋物線相切,僅有幾個交點,求得k的取值.
,即可求得拋物線截直線y=2x﹣6所得的弦長;(2)當k=0時,y=1,直線與拋物線有一個交點,當k≠0時,將y=kx+1代入拋物線方程,由△>0,直線與拋物線有兩個交點,求得k的取值范圍,當△<0,直線與拋物線相離,無交點,求得k的取值范圍,當△=0,直線與拋物線相切,僅有幾個交點,求得k的取值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() +m為奇函數,m為常數.
+m為奇函數,m為常數.
(1)求實數m的值;
(2)判斷并證明f(x)的單調性;
(3)若關于x的不等式f(f(x))+f(ma)<0有解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函數,求m的值
(2)用定義證明f(x)在R上單調遞增
(3)若f(x)值域為D,且D[﹣3,1],求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,棱長為a的正方體ABCD﹣A1B1C1D1中,點M,N,E分別是棱A1B1 , A1D1 , C1D1的中點. 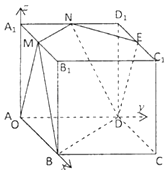
(1)過AM作一平面,使其與平面END平行(只寫作法,不需要證明);
(2)在如圖的空間直角坐標系中,求直線AM與平面BMND所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題p:x∈[1,12],x2﹣a≥0.命題q:x0∈R,使得x02+(a﹣1)x0+1<0.若p或q為真,p且q為假,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=x2+bx+4
(1)若f(x)為偶函數,求b的值;
(2)若f(x)有零點,求b的取值范圍;
(3)求f(x)在區間[﹣1,1]上的最大值g(b).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,其中實數
,其中實數![]() 為常數,
為常數,![]() 為自然對數的底數.
為自然對數的底數.
(1)當![]() 時,求函數
時,求函數![]() 的單調區間;
的單調區間;
(2)當![]() 時,解關于
時,解關于![]() 的不等式
的不等式![]() ;
;
(3)當![]() 時,如果函數
時,如果函數![]() 不存在極值點,求
不存在極值點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A=B=R,x∈A,y∈B,f:x→y=ax+b是從A到B的映射,若1和8的原象分別是3和10,則5在f下的象是( )
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某居民區隨機抽取10個家庭,獲得第i個家庭的月收入xi(單位:千元)與月儲蓄yi(單位:千元)的數據資料,算得 ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(Ⅰ)求家庭的月儲蓄y對月收入x的線性回歸方程y=bx+a;
(Ⅱ)判斷變量x與y之間是正相關還是負相關;
(Ⅲ)若該居民區某家庭月收入為7千元,預測該家庭的月儲蓄.
附:線性回歸方程y=bx+a中, 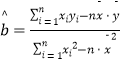 ,
, ![]() ,其中
,其中 ![]() ,
, ![]() 為樣本平均值,線性回歸方程也可寫為
為樣本平均值,線性回歸方程也可寫為 ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com