Question

【題目】已知圓經過兩點，且圓心在直線l：上．

Ⅰ求圓的方程；

Ⅱ求過點且與圓相切的直線方程；

Ⅲ設圓與x軸相交于A、B兩點，點P為圓上不同于A、B的任意一點，直線PA、PB交y軸于M、N點當點P變化時，以MN為直徑的圓是否經過圓內一定點？請證明你的結論．

Answer 1

【答案】（Ⅰ）；（Ⅱ）或；（Ⅲ）經過定點．

【解析】

Ⅰ設圓圓心為，由求得a的值，可得圓心坐標和半徑，從而求得圓的標準方程．

Ⅱ當切線斜率不存在時，求得的方程；當切線斜率存在時，設切線：，由圓心到切線的距離等于半徑求得k的值，可得切線的方程．

Ⅲ設，由條件求得M、N的坐標，可得圓的方程再根據定點在x軸上，求出定點的坐標．

解：Ⅰ法一：設圓圓心為，由得，，

解得，，半徑為，

所以圓：．

Ⅱ當切線斜率不存在時，：．

當切線斜率存在時，設切線：，

即，由圓心到切線的距離，

解得，此時：．

綜上：：或

Ⅲ設，則．

又，，

所以：，，：，

圓的方程為．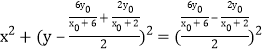

化簡得．

由動點關于x軸的對稱性可知，定點必在x軸上，令，得．

又點在圓內，

所以當點P變化時，以MN為直徑的圓經過定點．