【題目】對于給定的大于1的正整數n，設
，其中
，且
記滿足條件的所有x的和為
，
（1）求
（2）設
，求
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費用支出x萬元與銷售額y萬元之間有如下的對應數據：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）畫出散點圖；
（2）求回歸直線方程；
（3）據此估計廣告費用為12萬元時，銷售收入y的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P﹣ABC中，D，E分別是BC，AB的中點，PA⊥平面ABC，∠BAC=90°，AB≠AC，AC＞AD，PC與DE所成的角為α，PD與平面ABC所成的角為β，二面角P﹣BC﹣A的平面角為γ，則α，β，γ的大小關系是（ ） 
A.α＜β＜γ
B.α＜γ＜β
C.β＜α＜γ
D.γ＜β＜α
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知x0 ， x0+ 
是函數f（x）=cos2（wx﹣ 
）﹣sin2wx（ω＞0）的兩個相鄰的零點
（1）求 
的值；
（2）若對 
，都有|f（x）﹣m|≤1，求實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在三棱錐P﹣ABC中，D為AB的中點．
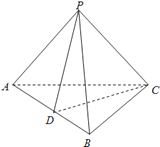
（1）與BC平行的平面PDE交AC于點E，判斷點E在AC上的位置并說明理由如下：
（2）若PA=PB，且△PCD為銳角三角形，又平面PCD⊥平面ABC，求證：AB⊥PC．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】射擊測試有兩種方案，方案1：先在甲靶射擊一次，以后都在乙靶射擊；方案2：始終在乙靶射擊，某射手命中甲靶的概率為
，命中一次得3分；命中乙靶的概率為
，命中一次得2分，若沒有命中則得0分，用隨機變量
表示該射手一次測試累計得分，如果的值不低于3分就認為通過測試，立即停止射擊；否則繼續射擊，但一次測試最多打靶3次，每次射擊的結果相互獨立。
（1）如果該射手選擇方案1，求其測試結束后所得分的分布列和數學期望E；
（2）該射手選擇哪種方案通過測試的可能性大？請說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，A，B，C是橢圓M：
上的三點，其中點A是橢圓的右頂點，BC過橢圓M的中心，且滿足AC⊥BC，BC＝2AC。
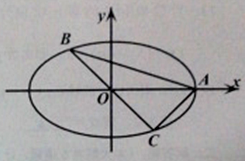
（1）求橢圓的離心率；
（2）若y軸被△ABC的外接圓所截得弦長為9，求橢圓方程。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分14分）
已知拋物線
的焦點為
， 
為
上異于原點的任意一點，過點
的直線
交
于另一點
，交
軸的正半軸于點
，且有
.當點
的橫坐標為
時， 
為正三角形.
（Ⅰ）求
的方程；
（Ⅱ）若直線
，且
和
有且只有一個公共點
，
（ⅰ）證明直線
過定點，并求出定點坐標；
（ⅱ）
的面積是否存在最小值？若存在，請求出最小值；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量 
=（3，﹣4）， 
=（6，﹣3）， 
=（5﹣x，﹣3﹣y）， 
=（4，1）
（1）若四邊形ABCD是平行四邊形，求x，y的值；
（2）若△ABC為等腰直角三角形，且∠B為直角，求x，y的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
