
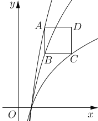
【題目】如果,已知正方形![]() 的邊長為2,
的邊長為2,![]() 平行
平行![]() 軸,頂點
軸,頂點![]() ,
,![]() 和
和![]() 分別在函數
分別在函數![]() ,
,![]() 和
和![]() 的圖像上,則實數
的圖像上,則實數![]() 的值為________
的值為________
科目:高中數學 來源: 題型:
【題目】對于兩個定義域相同的函數![]() 、
、![]() ,若存在實數
,若存在實數![]() 、
、![]() 使
使![]() ,則稱函數
,則稱函數![]() 是由“基函數
是由“基函數![]() 、
、![]() ”生成的.
”生成的.
(1)![]() 和
和![]() 生成一個偶函數
生成一個偶函數![]() ,求
,求![]() 的值;
的值;
(2)若![]() 由
由![]() ,
,![]() (
(![]() 且
且![]() )生成,求
)生成,求![]() 的取值范圍;
的取值范圍;
(3)試利用“基函數![]() ,
,![]() ”生成一個函數
”生成一個函數![]() ,使
,使![]() 滿足下列條件:①是偶函數;②有最小值1,請求出函數
滿足下列條件:①是偶函數;②有最小值1,請求出函數![]() 的解析式并進一步研究該函數的單調性(無需證明).
的解析式并進一步研究該函數的單調性(無需證明).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在一項自“一帶一路”沿線20國青年參與的評選中“高鐵”、“支付寶”、“共享單車”和“網購”被稱作中國“新四大發明”,曾以古代“四大發明”推動世界進步的中國,正再次以科技創新向世界展示自己的發展理念.某班假期分為四個社會實踐活動小組,分別對“新四大發明”對人們生活的影響進行調查.于開學進行交流報告會.四個小組隨機排序,則“支付寶”小組和“網購”小組不相鄰的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f (x)=x-(a+1)ln x-![]() (a∈R),g (x)=
(a∈R),g (x)=![]() x2+ex-xex.
x2+ex-xex.
(1)當x∈[1,e] 時,求f (x)的最小值;
(2)當a<1時,若存在x1∈[e,e2],使得對任意的x2∈[-2,0],f (x1)<g (x2)恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
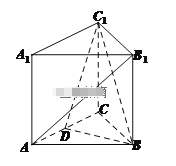
【題目】如圖,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,且
,且![]() 為正三角形,
為正三角形,![]() ,
,![]() 為
為![]() 的中點.
的中點.
(1)求證:直線![]() 平面
平面![]() ;
;
(2)求三棱錐![]() 的體積;
的體積;
(3)三棱柱![]() 的頂點都在一個球面上,求該球的體積.
的頂點都在一個球面上,求該球的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象經過點
的圖象經過點![]() ,且在區間
,且在區間![]() 上單調遞減,在
上單調遞減,在![]() 上單調遞增.
上單調遞增.
(Ⅰ)證明![]() ;
;
(Ⅱ)求![]() 的解析式;
的解析式;
(Ⅲ)若對于任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,試問:這樣的
恒成立,試問:這樣的![]() 是否存在,若存在,請求出
是否存在,若存在,請求出![]() 的范圍;若不存在,說明理由.
的范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某市準備在道路EF的一側修建一條運動比賽道,賽道的前一部分為曲線段FBC.該曲線段是函數![]() 時的圖象,且圖象的最高點為B
時的圖象,且圖象的最高點為B![]() 賽道的中間部分為長
賽道的中間部分為長![]() 千米的直線跑道CD,且CD∥EF;賽道的后一部分是以
千米的直線跑道CD,且CD∥EF;賽道的后一部分是以![]() 為圓心的一段圓弧DE.
為圓心的一段圓弧DE.

(1)求![]() 的值和∠DOE的大小;
的值和∠DOE的大小;
(2)若要在圓弧賽道所對應的扇形ODE區域內建一個“矩形草坪”,矩形的一邊在道路EF上,一個頂點在半徑OD上,另外一個頂點P在圓弧DE上,求“矩形草坪”面積的最大值,并求此時P點的位置.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com