
在數列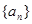 中,
中,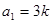 ,其中
,其中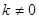 ,對任意
,對任意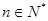 都有:
都有: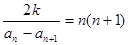 ;(1)求數列
;(1)求數列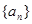 的第2項和第3項;
的第2項和第3項;
(2)求數列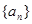 的通項公式
的通項公式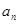 ,假設
,假設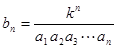 ,試求數列
,試求數列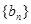 的前
的前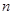 項和
項和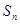 ;
;
(3)若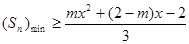 對一切
對一切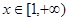 恒成立,求
恒成立,求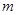 的取值范圍。
的取值范圍。
【解析】第一問中利用)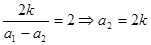 同理得到
同理得到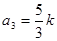
第二問中,由題意得到: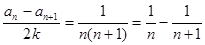
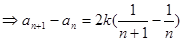
累加法得到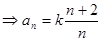
第三問中,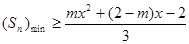 利用恒成立,轉化為最小值大于等于即可。得到范圍。
利用恒成立,轉化為最小值大于等于即可。得到范圍。
(1)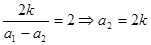 同理得到
同理得到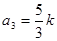 ……2分
……2分
(2)由題意得到: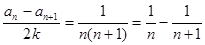
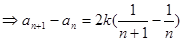
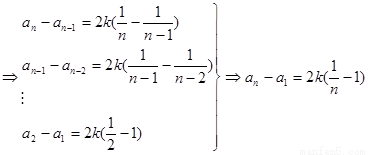 又
又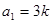
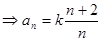 ……5分
……5分
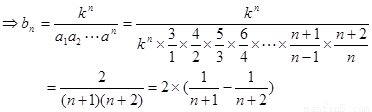
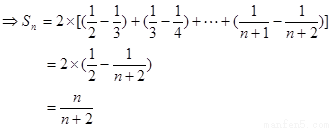 ……8分
……8分
(3)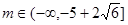
 云南師大附小一線名師提優作業系列答案
云南師大附小一線名師提優作業系列答案 沖刺100分單元優化練考卷系列答案
沖刺100分單元優化練考卷系列答案科目:高中數學 來源:2007年普通高等學校招生全國統一考試文科數學卷(天津) 題型:解答題
(本小題滿分14分)
在數列 中,
中, ,其中
,其中 .
.
(Ⅰ)求數列 的通項公式;
的通項公式;
(Ⅱ)求數列 的前
的前 項和
項和 ;
;
(Ⅲ)證明存在 ,使得
,使得 對任意
對任意 均成立.
均成立.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三下學期開學考試理科數學 題型:解答題
(本題滿分14分)在數列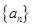 中,
中, ,其中
,其中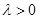 .
.
(Ⅰ)求數列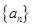 的通項公式;
的通項公式;
(Ⅱ)求數列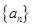 的前
的前 項和
項和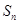 ;
;
(Ⅲ)證明存在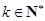 ,使得
,使得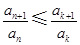 對任意
對任意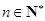 均成立.
均成立.
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試文科數學卷(天津) 題型:解答題
(本小題滿分14分)
在數列 中,
中,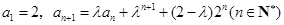 ,其中
,其中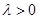 .
.
(Ⅰ)求數列 的通項公式;
的通項公式;
(Ⅱ)求數列 的前
的前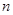 項和
項和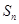 ;
;
(Ⅲ)證明存在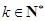 ,使得
,使得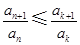 對任意
對任意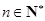 均成立.
均成立.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com