Question

(2005山東，22)如下圖,已知動圓過定點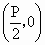，且與直線相切，其中p＞0，

(1)求動圓圓心的軌跡C的方程；

(2)設A、B是軌跡C上異于原點O的兩個不同點，直線OA和OB的傾斜角分別為α和β，當α、β變化且α+β為定值θ(0＜θ＜π)時，證明：直線AB恒過定點，并求出該定點的坐標．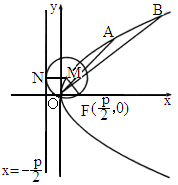

Answer 1

答案：略
解析：

解析：(1)設M為動圓圓心，記為F，過點M作直線的垂線，垂足為N． 由題意知：，即動點M到定點F與定直線的距離相等，由拋物線定義知：點M的軌跡為拋物線，其中為焦點，為準線，所以軌跡方程為． (2)設，由題意得(否則)且． 所以直線AB的斜率存在，設其方程為y=kx＋b． 顯然．將y=kx＋b與聯立消去x，得． 由韋達定理知 ．　　　　(*) ①當時，即時， ， ， ． 由(*)式知：． 因此直線AB的方程可表示為： ，即k(x＋2p)－y=0． ∴直線AB恒過定點(－2p，0)． ②當，由得 ． 將(*)式代入上式整理化簡，得： ． 此時，直線AB的方程可表示為， 即． ∴直線AB恒過定點． ∴由①②知， 當時，直線AB恒過定點(－2p，0)； 當時，直線AB恒過定點．