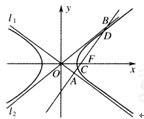
如圖,雙曲線的中心在坐標原點O,焦點在x軸上,兩條漸近線分別為l
1,l
2,經過右焦點F垂直于l
1的直線分別交l
1,l
2于A,B兩點.又已知該雙曲線的離心率
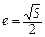
.
(1)求證:
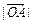
,
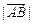
,
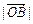
依次成等差數(shù)列;
(2)若F(
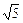
,0),求直線AB在雙曲線上所截得的弦CD的長度.
解:(1)由已知e2=
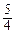
,即
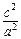
=
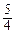
,故a2=
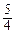
c2, ①
從而b2=c2-a2=
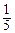
c2, ②
故
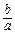
=
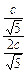
=
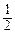
,設∠AOF=∠BOF=
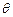
,
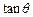
=
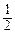
.
故tan∠AOB=tan2
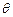
=

=
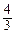
,即
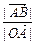
=
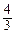
.
令
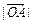
=3m(m>0) ,則
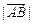
=4m,
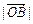
=5m,滿足
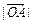
+
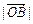
=2
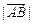
,
所以,
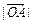
,
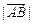
,
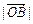
依次成等差數(shù)列.
(2)由已知c2=5,代入①,②得a2=4, b2=1,
于是雙曲線的方程為
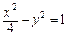
.
設直線AB的斜率為k,則k=tan∠BFx=tan∠AFO=cot
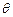
=2.
于是直線AB的議程為 y=2(x-
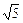
).…………………………………………9分
聯(lián)立

消y得15x2-
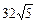
x+84=0.
故弦CD的長度 | CD |=
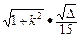
=
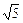
×
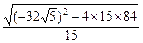
=
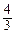
…13分
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:單選題
設雙曲線
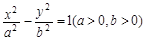
的離心率為
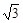
,且它的一條準線與拋物線
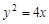
的準線重合,則此雙曲線的方程為
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知雙曲線
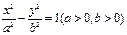
的兩個焦點分別為
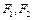
,過作垂直于x軸的直線,
與雙曲線的一個交點為P,且
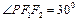
,則雙曲線的離心率為( )
| A.2 | B.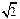 | C.3 | D.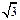 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線
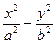
=1(
a>0,
b>0)的半焦距為
c,若
b2-4
ac<0,則它的離心率的取值范圍是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線
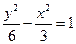
,則以雙曲線中心為頂點,以雙曲線準線為準線的拋物線方程為.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知雙曲線的中心在坐標原點,一個焦點為
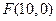
,兩條漸近線的方程為
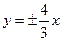
,則該雙曲線的標準方程為
▲ .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
雙曲線
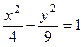
上一點P到它的一個焦點的距離等于5,那么點P到另一個焦點的距離等于________________
查看答案和解析>>

 .
.
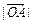 ,
,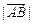 ,
,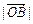 依次成等差數(shù)列;
依次成等差數(shù)列;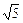 ,0),求直線AB在雙曲線上所截得的弦CD的長度.
,0),求直線AB在雙曲線上所截得的弦CD的長度. 黃岡創(chuàng)優(yōu)卷系列答案
黃岡創(chuàng)優(yōu)卷系列答案