
如圖,三棱柱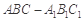 中,側棱與底面垂直,
中,側棱與底面垂直,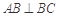 ,
,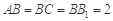 ,
,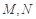 分別是
分別是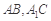 的中點
的中點
(1)求證: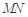 ∥平面
∥平面 ;
;
(2)求證: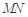 ⊥平面
⊥平面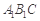 ;
;
(3)求三棱錐的體積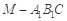 的體積.
的體積.
(1)證明過程詳見解析;(2)證明過程詳見解析;(3)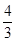 .
.
【解析】
試題分析:本題主要以三棱柱為幾何背景考查線面平行、線面垂直和幾何體體積等基礎知識,考查空間想象能力、運算能力和推理論證能力.第一問,先根據題意作出輔助線,在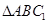 中,利用中位線的性質得
中,利用中位線的性質得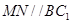 ,再由線面平行的判定,得證;第二問,由已知條件可以判斷四邊形
,再由線面平行的判定,得證;第二問,由已知條件可以判斷四邊形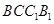 是正方形,所以對角線互相垂直,所以
是正方形,所以對角線互相垂直,所以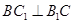 ,又由于第一問得
,又由于第一問得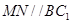 ,所以
,所以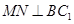 ,再由已知證
,再由已知證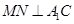 即可,由已知邊長,得
即可,由已知邊長,得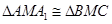 ,所以
,所以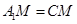 ,所以
,所以 為等腰三角形,而
為等腰三角形,而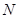 為中點,所以
為中點,所以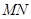 為高,得證,再利用線面垂直的判定即可得證;第三問,利用等體積法將三棱錐進行轉化,找到已知條件求體積.
為高,得證,再利用線面垂直的判定即可得證;第三問,利用等體積法將三棱錐進行轉化,找到已知條件求體積.
試題解析:(1)證明:連結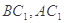 ,顯然
,顯然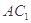 過點
過點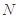
∵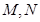 分別是
分別是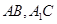 的中點, ∴
的中點, ∴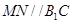 ,
,
又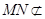 平面
平面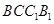 ,
,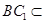 平面
平面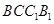 ,∴
,∴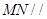 平面
平面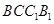 ,
,
(2)∵三棱柱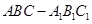 中,側棱與底面垂直,
中,側棱與底面垂直,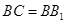 ,
,
∴四邊形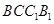 是正方形,∴
是正方形,∴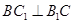 ,
,
由(1)知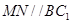 ,∴
,∴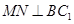 ,
,
連結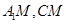 ,由
,由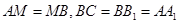 ,知
,知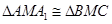 ,
,
∴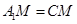 ,又易知
,又易知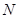 是
是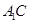 的中點,∴
的中點,∴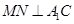 ,
,
∴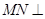 平面
平面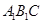 .
.
(3)因為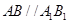 ,所以三棱錐
,所以三棱錐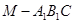 與三棱錐
與三棱錐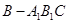 的體積相等,
的體積相等,
故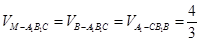 .
.
考點:1.中位線的性質;2.線面平行的判定;3.三角形全等;4.線面垂直的判定;5.等體積法.


 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源:2012-2013學年陜西西安高三第十二次適應性訓練文數學卷(解析版) 題型:解答題
如圖在三棱柱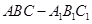 中,側棱
中,側棱 底面
底面 ,
,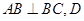 為
為 的中點,
的中點, 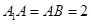 ,
,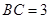 .
.

(1)求證: 平面
平面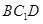 ;
;
(2)求四棱錐 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源:2011-2012年海南省高一上學期教學質量監測考試數學 題型:選擇題
如圖,三棱柱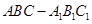 中,側棱
中,側棱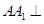 底面
底面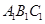 ,底面三角形
,底面三角形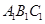 是正三角形,
是正三角形, 是
是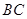 中點,則下列敘述正確的是:
中點,則下列敘述正確的是:
A.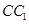 與
與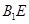 是異面直線
B.
是異面直線
B.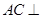 平面
平面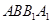
C.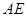 ,
,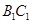 為異面直線,且
為異面直線,且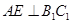 D.
D.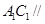 平面
平面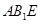
查看答案和解析>>
科目:高中數學 來源:2014屆寧夏中衛市海原一中高一上學期期末考試數學 題型:選擇題
如圖,三棱柱 中,側棱
中,側棱 底面
底面 ,底面三角形
,底面三角形 是正三角形,
是正三角形, 是
是 中點,則下列敘述正確的是( )
中點,則下列敘述正確的是( )


A. 與
與 是異面直線
是異面直線
B.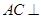 平面
平面
C. 平面
平面
D. ,
, 為異面直線,且
為異面直線,且
查看答案和解析>>
科目:高中數學 來源:2010年浙江省高二上學期10月月考數學卷 題型:選擇題
如圖,三棱柱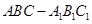 中,側棱
中,側棱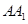 垂直底面
垂直底面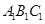 ,底面三角形
,底面三角形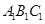 是正三角形,
是正三角形, 是
是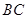 中點,則下列敘述正確的是( )
中點,則下列敘述正確的是( )
A.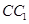 與
與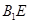 是異面直線
B.
是異面直線
B.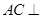 平面
平面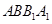
C.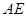 ,
,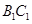 為異面直線,且
為異面直線,且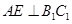 D.
D.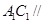 平面
平面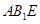
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com