
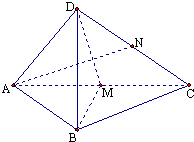
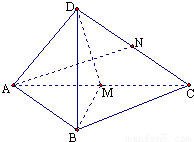
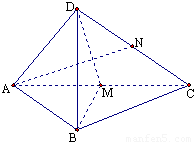
 四面體D-ABC,中,AB=BC,在側面DAC中,中線AN⊥中線DM,且DB⊥AN.
四面體D-ABC,中,AB=BC,在側面DAC中,中線AN⊥中線DM,且DB⊥AN.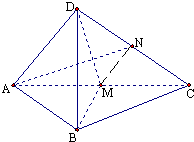
 AN×DM=6
AN×DM=6 S△CAD,
S△CAD, S△CAD=6,得S△CAD=8
S△CAD=6,得S△CAD=8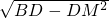 =4
=4 S△CAD×BM=
S△CAD×BM= .
. S△CAD=6,得S△CAD=8.用勾股定理算出BM的長,最后根據BM⊥平面ACD,結合錐體體積公式,可算出四面體D-ABC的體積.
S△CAD=6,得S△CAD=8.用勾股定理算出BM的長,最后根據BM⊥平面ACD,結合錐體體積公式,可算出四面體D-ABC的體積.

 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:
 如圖在四面體D-ABC中,OA、0B、OC兩兩垂直,且OB=OC=3,OA=4.給出以下判斷:
如圖在四面體D-ABC中,OA、0B、OC兩兩垂直,且OB=OC=3,OA=4.給出以下判斷:查看答案和解析>>
科目:高中數學 來源: 題型:
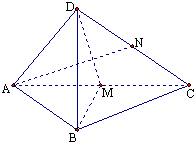 四面體D-ABC,中,AB=BC,在側面DAC中,中線AN⊥中線DM,且DB⊥AN.
四面體D-ABC,中,AB=BC,在側面DAC中,中線AN⊥中線DM,且DB⊥AN.查看答案和解析>>
科目:高中數學 來源:《立體幾何》2013年廣東省廣州大學附中高考數學二輪檢測(解析版) 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2012年寧夏高考數學仿真模擬試卷9(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com