
【題目】已知集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
)x﹣1≤9},集合B={x|log2x<3},集合C={x|x2﹣(2a+1)x+a2+a≤0},U=R
(1)求集合A∩B,(UB)∪A;
(2)若A∪C=A,求實數a的取值范圍.
【答案】
(1)解:由題意:U=R,
集合A={x| ![]() ≤(
≤( ![]() )x﹣1≤9}={x|﹣1≤x≤2};
)x﹣1≤9}={x|﹣1≤x≤2};
集合B={x|log2x<3}={x|0<x<8};
則:UB={x|0≥x或8≤x};
集合C={x|x2﹣(2a+1)x+a2+a≤0}={x|a≤x≤a+1}
∴集合A∩B={x|0<x≤2};
(UB)∪A={x|x≤2或8≤x}
(2)解:由題意:A∪C=A,
∴CA,
則滿足: ![]() ,
,
解得:﹣1≤a≤1
所以實數a的取值范圍是[﹣1,1]
【解析】(1)確定集合A,集合B的組成范圍,根據集合的基本運算即可求A∩B,(UB)∪A;(2)根據A∪C=A,建立條件關系即可求實數a的取值范圍.
【考點精析】本題主要考查了交、并、補集的混合運算的相關知識點,需要掌握求集合的并、交、補是集合間的基本運算,運算結果仍然還是集合,區分交集與并集的關鍵是“且”與“或”,在處理有關交集與并集的問題時,常常從這兩個字眼出發去揭示、挖掘題設條件,結合Venn圖或數軸進而用集合語言表達,增強數形結合的思想方法才能正確解答此題.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】如圖1:已知正方形ABCD的邊長是2,有一動點M從點B出發沿正方形的邊運動,路線是B→C→D→A.設點M經過的路程為x,△ABM的面積為S. 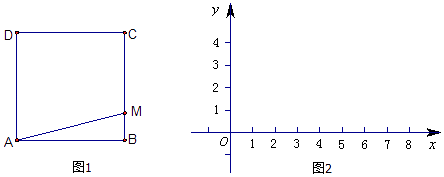
(1)求函數S=f(x)的解析式及其定義域;
(2)在圖2中畫出函數S=f(x)的圖象.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() (
(![]() 為自然對數的底數),
為自然對數的底數),![]() ,
, ![]() .
.
(1)若![]() 是
是![]() 的極值點,且直線
的極值點,且直線![]() 分別與函數
分別與函數![]() 和
和![]() 的圖象交于
的圖象交于![]() ,求
,求![]() 兩點間的最短距離;
兩點間的最短距離;
(2)若![]() 時,函數
時,函數![]() 的圖象恒在
的圖象恒在![]() 的圖象上方,求實數
的圖象上方,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是指企業在校園、地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務,是共享經濟的一種新形態.一個共享單車企業在某個城市就“一天中一輛單車的平均成本(單位:元)與租用單車的數量(單位:千輛)之間的關系”進行調查研究,在調查過程中進行了統計,得出相關數據見下表:
租用單車數量 | 2 | 3 | 4 | 5 | 8 |
每天一輛車平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 |
根據以上數據,研究人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲: ![]() ,方程乙:
,方程乙: ![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務:
①完成下表(計算結果精確到0.1)(備注: ![]() ,
,![]() 稱為相應于點
稱為相應于點![]() 的殘差(也叫隨機誤差));
的殘差(也叫隨機誤差));
租用單車數量 | 2 | 3 | 4 | 5 | 8 | |
每天一輛車平均成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估計值 | 2.4 | 2.1 | 1.6 | ||
殘差 | 0 | -0.1 | 0.1 | |||
模型乙 | 估計值 | 2.3 | 2 | 1.9 | ||
殘差 | 0.1 | 0 | 0 | |||
②分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(2)這個公司在該城市投放共享單車后,受到廣大市民的熱烈歡迎,共享單車常常供不應求,于是該公司研究是否增加投放.根據市場調查,這個城市投放8千輛時,該公司平均一輛單車一天能收入10元,6元收入的概率分別為0.6,0.4;投放1萬輛時,該公司平均一輛單車一天能收入10元,6元收入的概率分別為0.4,0.6.問該公司應該投放8千輛還是1萬輛能獲得更多利潤?(按(1)中擬合效果較好的模型計算一天中一輛單車的平均成本,利潤=收入-成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=|lnx|,若函數g(x)=f(x)﹣ax在區間(0,3]上有三個零點,則實數a的取值范圍是( )
A.(0, ![]() )
)
B.( ![]() ,e)
,e)
C.(0, ![]() ]
]
D.[ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+
,若方程f(x)=a有四個不同的解x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 則x3(x1+x2)+ ![]() 的取值范圍是( )
的取值范圍是( )
A.(﹣1,+∞)
B.(﹣1,1]
C.(﹣∞,1)
D.[﹣1,1)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|mx|﹣|x﹣n|(0<n<1+m),若關于x的不等式f(x)<0的解集中的整數恰有3個,則實數m的取值范圍為( )
A.3<m<6
B.1<m<3
C.0<m<1
D.﹣1<m<0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com