
【題目】已知函數![]() .
.
(1)討論![]() 的單調性;
的單調性;
(2)若![]() 為
為![]() 的兩個極值點,證明:
的兩個極值點,證明:![]() .
.
科目:高中數學 來源: 題型:
【題目】某學校為調查高三年級學生的身高情況,按隨機抽樣的方法抽取80名學生,得到男生身高情況的頻率分布直方圖(如圖(1))和女生身高情況的頻率分布直方圖(如圖(2)).已知圖(1)中身高在170~175cm的男生有16名.
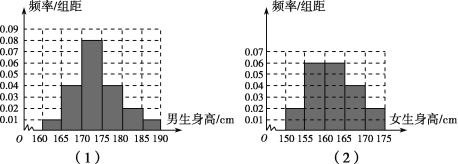
(1)試問在抽取的學生中,男、女生各有多少名?
身高≥170cm | 身高<170cm | 總計 | |
男生 | |||
女生 | |||
總計 |
(2)根據頻率分布直方圖,完成下面的2×2列聯表,并判斷能有多大(百分數)的把握認為身高與性別有關?
附:參考公式和臨界值表
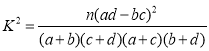
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4―4:坐標系與參數方程]
在直角坐標系xOy中,曲線C的參數方程為![]() (θ為參數),直線l的參數方程為
(θ為參數),直線l的參數方程為![]() .
.
(1)若a=1,求C與l的交點坐標;
(2)若C上的點到l的距離的最大值為![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() (
(![]() )的上頂點為
)的上頂點為![]() ,圓
,圓![]() 經過點
經過點![]() .
.
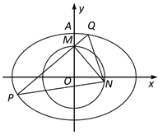
(1)求橢圓![]() 的方程;
的方程;
(2)過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,過點
兩點,過點![]() 作直線
作直線![]() 的垂線
的垂線![]() 交圓
交圓![]() 于另一點
于另一點![]() .若△PQN的面積為3,求直線
.若△PQN的面積為3,求直線![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程選講
在平面直角坐標系中,以原點為極點,以![]() 軸非負半軸為極軸建立極坐標系, 已知曲線
軸非負半軸為極軸建立極坐標系, 已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)寫出曲線![]() 和直線
和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 過點
過點![]() 與曲線
與曲線![]() 交于不同兩點
交于不同兩點![]() ,
,![]() 的中點為
的中點為![]() ,
,![]() 與
與![]() 的交點為
的交點為![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】菜農定期使用低害殺蟲農藥對蔬菜進行噴灑,以防止害蟲的危害,但采集上市時蔬菜仍存有少量的殘留農藥,食用時需要用清水清洗干凈,下表是用清水x(單位:千克)清洗該蔬菜1千克后,蔬菜上殘留的農藥y(單位:微克)的數據作了初步處理,得到下面的散點圖及一些統計量的值.
y(微克)
 x(千克)
x(千克)
|
|
|
|
|
|
|
3 | 38 | 11 | 10 | 374 | -121 | -751 |
其中![]()
(I)根據散點圖判斷,![]() 與
與![]() ,哪一個適宜作為蔬菜農藥殘量
,哪一個適宜作為蔬菜農藥殘量![]() 與用水量
與用水量![]() 的回歸方程類型(給出判斷即可,不必說明理由);
的回歸方程類型(給出判斷即可,不必說明理由);
(Ⅱ)若用解析式![]()
![]() 與用水量
與用水量![]() 的回歸方程,求出
的回歸方程,求出![]() 與
與![]() 的回歸方程.(c,d精確到0.1)
的回歸方程.(c,d精確到0.1)
(Ⅲ)對于某種殘留在蔬菜上的農藥,當它的殘留量低于20微克時對人體無害,為了放心食用該蔬菜,請估計需要用多少千克的清水清洗一千克蔬菜?(精確到0.1,參考數據![]() )
)
附:參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:x2+y2+2x﹣4y+3=0.
(1)若直線l:x+y=0與圓C交于A,B兩點,求弦AB的長;
(2)從圓C外一點P(x1,y1)向該圓引一條切線,切點為M,O為坐標原點,且有|PM|=|PO|,求使得|PM|取得最小值的點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市教育局衛生健康所對全市高三年級的學生身高進行抽樣調查,隨機抽取了100名學生,他們身高都處于![]() 五個層次,根據抽樣結果得到如下統計圖表,則從圖表中不能得出的信息是( )
五個層次,根據抽樣結果得到如下統計圖表,則從圖表中不能得出的信息是( )
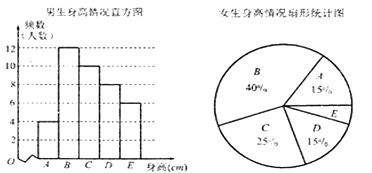
A. 樣本中男生人數少于女生人數
B. 樣本中![]() 層次身高人數最多
層次身高人數最多
C. 樣本中![]() 層次身高的男生多于女生
層次身高的男生多于女生
D. 樣本中![]() 層次身高的女生有3人
層次身高的女生有3人
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com