
【題目】某日用品按行業質量標準分成五個等級,等級系數X依次為1,2,3,4,5.現從一批該日用品中隨機抽取20件,對其等級系數進行統計分析,得到頻率分布表如下:
X | 1 | 2 | 3 | 4 | 5 |
頻率 | a | 0.2 | 0.45 | b | c |
(1)若所抽取的20件日用品中,等級系數為4的恰有3件,等級系數為5的恰有2件,求a,b,c的值;
(2)在(1)的條件下,將等級系數為4的3件日用品記為![]() ,等級系數為5的2件日用品記為
,等級系數為5的2件日用品記為![]() ,現從
,現從![]() ,
, ![]() 這5件日用品中任取兩件(假定每件日用品被取出的可能性相同),求這兩件日用品的等級系數恰好相等的概率.
這5件日用品中任取兩件(假定每件日用品被取出的可能性相同),求這兩件日用品的等級系數恰好相等的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,
(1)若函數![]() 的兩個極值點為
的兩個極值點為![]() ,求函數
,求函數![]() 的解析式;
的解析式;
(2)在(1)的條件下,求函數![]() 的圖象過點
的圖象過點![]() 的切線方程;
的切線方程;
(3)對一切![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:
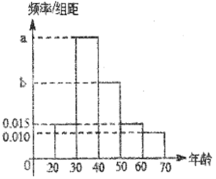
【題目】根據某電子商務平臺的調查統計顯示,參與調查的1000位上網購物者的年齡情況如圖.
(1)已知![]() 、
、![]() ,
,![]() 三個年齡段的上網購物者人數成等差數列,求
三個年齡段的上網購物者人數成等差數列,求![]() ,
,![]() 的值;
的值;
(2)該電子商務平臺將年齡在![]() 之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發放代金券,高消費人群每人發放50元的代金券,潛在消費人群每人發放80元的代金券.已經采用分層抽樣的方式從參與調查的1000位上網購物者中抽取了10人,現在要在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和
之間的人群定義為高消費人群,其他的年齡段定義為潛在消費人群,為了鼓勵潛在消費人群的消費,該平臺決定發放代金券,高消費人群每人發放50元的代金券,潛在消費人群每人發放80元的代金券.已經采用分層抽樣的方式從參與調查的1000位上網購物者中抽取了10人,現在要在這10人中隨機抽取3人進行回訪,求此三人獲得代金券總和![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形ABCD為正方形, ![]() 為直角三角形,
為直角三角形, ![]() ,且
,且![]() .
.
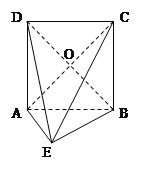
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若AB=2AE,求異面直線BE與AC所成角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=Asin(ωx+φ)(A>0,ω>0)的圖象過點P![]() ,圖象與P點最近的一個最高點坐標為
,圖象與P點最近的一個最高點坐標為![]() .
.
(1)求函數解析式;
(2)求函數的最大值,并寫出相應的x的值;
(3)求使y≤0時,x的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知|a|=4,|b|=3,(2a-3b)·(2a+b)=61,
(1)求a與b的夾角θ; (2)求|a+b|;
(3)若![]() =a,
=a, ![]() =b,求△ABC的面積.
=b,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國上是世界嚴重缺水的國家,城市缺水問題較為突出,某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準![]() (噸),用水量不超過
(噸),用水量不超過![]() 的部分按平價收費,超過
的部分按平價收費,超過![]() 的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照
的部分按議價收費,為了了解全市民月用水量的分布情況,通過抽樣,獲得了100位居民某年的月用水量(單位:噸),將數據按照![]() ,
, ![]() ,…,
,…, ![]() 分成9組,制成了如圖所示的頻率分布直方圖.
分成9組,制成了如圖所示的頻率分布直方圖.
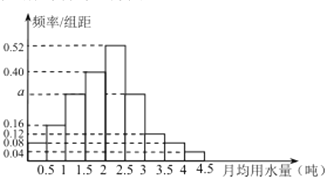
(Ⅰ)求直方圖中![]() 的值;
的值;
(Ⅱ)已知該市有80萬居民,估計全市居民中月均用水量不低于3噸的人數,并說明理由;
(Ⅲ)若該市政府希望使![]() 的居民每月的用水量不超過標準
的居民每月的用水量不超過標準![]() (噸),估計
(噸),估計![]() 的值,并說明理由;
的值,并說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在![]() 上的單調遞減函數
上的單調遞減函數![]() ,對任意
,對任意![]() 都有
都有![]() ,
, ![]() .
.
(Ⅰ)判斷函數![]() 的奇偶性,并證明之;
的奇偶性,并證明之;
(Ⅱ)若對任意![]() ,不等式
,不等式![]() (
(![]() 為常實數)都成立,求
為常實數)都成立,求![]() 的取值范圍;(Ⅲ)設
的取值范圍;(Ⅲ)設![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
若![]()
![]()
![]() ,
, ![]() ,比較
,比較![]() 的大小并說明理由.
的大小并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com