
已知m=a+![]() (a>2),n=
(a>2),n=![]() (x<0),則m與n的大小關系為( )
(x<0),則m與n的大小關系為( )
(A)m≤n (B)m<n (C)m≥n (D)m>n
科目:高中數學 來源: 題型:
(06年江西卷理)(12分)
如圖,已知△ABC是邊長為1的正三角形,M、N分別是
邊AB、AC上的點,線段MN經過△ABC的中心G,
設ÐMGA=a(![]() )
)
(1)試將△AGM、△AGN的面積(分別記為S1與S2)表示為a的函數
(2)求y=![]() 的最大值與最小值
的最大值與最小值

查看答案和解析>>
科目:高中數學 來源:2013-2014學年廣東汕頭市高一10月月考數學試卷(解析版) 題型:解答題
已知函數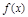 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若方程f(x)=0在[-1,1]上有實數根,求實數a的取值范圍;
(Ⅱ)當a=0時,若對任意的x1∈[1,4],總存在x2∈[1,4],使f(x1)=g(x2)成立,求實數m的取值范圍;
(Ⅲ)若函數y=f(x)(x∈[t,4])的值域為區間D,是否存在常數t,使區間D的長度為7-2t?若存在,求出t的值;若不存在,請說明理由(注:區間[p,q]的長度為q-p).
查看答案和解析>>
科目:高中數學 來源:2011-2012學年大綱版高三上學期單元測試(4)數學試卷 題型:解答題
如圖,已知△ABC是邊長為1的正三角形,M、N分別是邊AB、AC上的點,
線段MN經過△ABC的中心G,設ÐMGA=a( ).
).

(1)試將△AGM、△AGN的面積(分別記為S1與S2)表示為a的函數;
(2)求y= 的最大值與最小值.
的最大值與最小值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年本溪縣高三暑期補課階段考試數學卷 題型:解答題
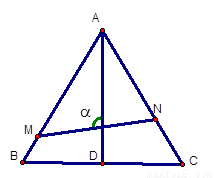
(本題12分)如圖,已知△ABC是邊長為1的正三角形,M、N分別是
邊AB、AC上的點,線段MN經過△ABC的中心G,設ÐMGA=a(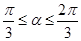 )
)
(1)試將△AGM、△AGN的面積(分別記為S1與S2)表示為a的函數
(2)求y=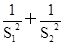 的最大值與最小值
的最大值與最小值
查看答案和解析>>
科目:高中數學 來源:2010-2011學年本溪縣高三暑期補課階段考試數學卷 題型:解答題
(本題12分)如圖,已知△ABC是邊長為1的正三角形,M、N分別是
邊AB、AC上的點,線段MN經過△ABC的中心G,設ÐMGA=a( )
)
(1)試將△AGM、△AGN的面積(分別記為S1與S2)表示為a的函數
(2)求y= 的最大值與最小值
的最大值與最小值

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com