
【題目】已知定義在[﹣ ![]() ,
, ![]() ]的函數f(x)=sinx(cosx+1)﹣ax,若y=f(x)僅有一個零點,則實數a的取值范圍是( )
]的函數f(x)=sinx(cosx+1)﹣ax,若y=f(x)僅有一個零點,則實數a的取值范圍是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
【答案】B
【解析】解:令g(x)=sinx(cosx+1),
則g′(x)=(2cosx﹣1)(cosx+1),
當x∈[﹣ ![]() ,﹣
,﹣ ![]() )時,g′(x)<0,g(x)為減函數,
)時,g′(x)<0,g(x)為減函數,
當x∈(﹣ ![]() ,
, ![]() )時,g′(x)>0,g(x)為增函數,
)時,g′(x)>0,g(x)為增函數,
當x∈( ![]() ,
, ![]() ]時,g′(x)<0,g(x)為減函數,
]時,g′(x)<0,g(x)為減函數,
故g(x)=sinx(cosx+1)的圖象如下圖所示: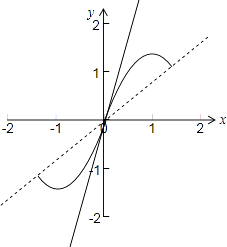
當x=± ![]() 時,g(x)=±1,此時a=
時,g(x)=±1,此時a= ![]() ,
,
當x=0時,g′(x)=2,
若y=f(x)僅有一個零點,
則函數g(x)=sinx(cosx+1)的圖象與y=ax的圖象有且僅有一個交點,
由圖可得:a∈(﹣∞, ![]() )∪[2,+∞),
)∪[2,+∞),
故選:B
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減).
在這個區間單調遞減).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,四邊形![]() 為等腰梯形,
為等腰梯形, ![]() ,
, ![]() ,
, ![]() ,四邊形
,四邊形![]() 為正方形,平面
為正方形,平面![]() 平面
平面![]() .
.

(1)若點![]() 是棱
是棱![]() 的中點,求證:
的中點,求證: ![]() 平面
平面![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=xlnx,g(x)= ![]() .
.
(Ⅰ)記F(x)=f(x)﹣g(x),判斷F(x)在區間(1,2)內零點個數并說明理由;
(Ⅱ)記(Ⅰ)中的F(x)在(1,2)內的零點為x0 , m(x)=min{f(x),g(x)},若m(x)=n(n∈R)在(1,+∞)有兩個不等實根x1 , x2(x1<x2),判斷x1+x2與2x0的大小,并給出對應的證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學為了普及奧運會知識和提高學生參加體育運動的積極性,舉行了一次奧運知識競賽.隨機抽取了30名學生的成績,繪成如圖所示的莖葉圖,若規定成績在75分以上(包括75分)的學生定義為甲組,成績在75分以下(不包括75分)定義為乙組.
(Ⅰ)在這30名學生中,甲組學生中有男生7人,乙組學生中有女生12人,試問有沒有90%的把握認為成績分在甲組或乙組與性別有關;
(Ⅱ)記甲組學生的成績分別為x1 , x2 , …,x12 , 執行如圖所示的程序框圖,求輸出的S的值;
(Ⅲ)競賽中,學生小張、小李同時回答兩道題,小張答對每道題的概率均為 ![]() ,小李答對每道題的概率均為
,小李答對每道題的概率均為 ![]() ,兩人回答每道題正確與否相互獨立.記小張答對題的道數為a,小李答對題的道數為b,X=|a﹣b|,寫出X的概率分布列,并求出X的數學期望.
,兩人回答每道題正確與否相互獨立.記小張答對題的道數為a,小李答對題的道數為b,X=|a﹣b|,寫出X的概率分布列,并求出X的數學期望.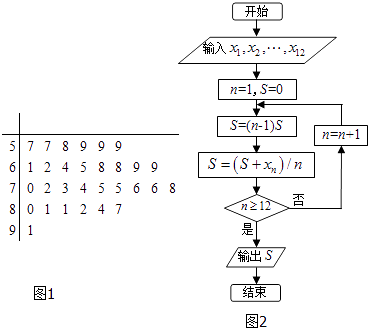
附:K2= ![]() ;其中n=a+b+c+d
;其中n=a+b+c+d
獨立性檢驗臨界表:
P(K2>k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知實數a>0,b>0,函數f(x)=|x﹣a|﹣|x+b|的最大值為3.
(I) 求a+b的值;
(Ⅱ)設函數g(x)=﹣x2﹣ax﹣b,若對于x≥a均有g(x)<f(x),求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
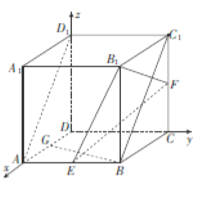
【題目】如圖,在正方體![]() 中,
中, ![]() 分別是棱
分別是棱![]() 的中點,
的中點, ![]() 為棱
為棱![]() 上一點,且異面直線
上一點,且異面直線![]() 與
與![]() 所成角的余弦值為
所成角的余弦值為![]() .
.
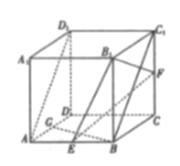
(1)證明: ![]() 為
為![]() 的中點;
的中點;
(2)求平面![]() 與平面
與平面![]() 所成銳二面角的余弦值.
所成銳二面角的余弦值.
【答案】(1)見解析(2)![]()
【解析】試題分析:(1)以![]() 為坐標原點,建立如圖所示的空間直角坐標系
為坐標原點,建立如圖所示的空間直角坐標系![]() ,不妨令正方體的棱長為2,設
,不妨令正方體的棱長為2,設![]() ,利用
,利用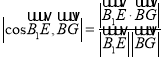 ,解得
,解得![]() ,即可證得;
,即可證得;
(2)分別求得平面![]() 與平面
與平面![]() 的法向量
的法向量![]() ,利用
,利用![]() 求解即可.
求解即可.
試題解析:
(1)證明:以![]() 為坐標原點,建立如圖所示的空間直角坐標系
為坐標原點,建立如圖所示的空間直角坐標系![]() .
.
不妨令正方體的棱長為2,
則![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
設![]() ,則
,則![]() ,
, ![]() ,
,
所以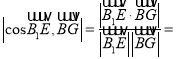
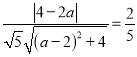 ,
,
所以![]() ,解得
,解得![]() (
(![]() 舍去),即
舍去),即![]() 為
為![]() 的中點.
的中點.
(2)解:由(1)可得![]() ,
, ![]() ,
,
設![]() 是平面
是平面![]() 的法向量,
的法向量,
則![]() .令
.令![]() ,得
,得![]() .
.
易得平面![]() 的一個法向量為
的一個法向量為![]() ,
,
所以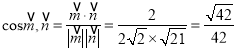 .
.
所以所求銳二面角的余弦值為![]() .
.
點睛:空間向量解答立體幾何問題的一般步驟是:(1)觀察圖形,建立恰當的空間直角坐標系;(2)寫出相應點的坐標,求出相應直線的方向向量;(3)設出相應平面的法向量,利用兩直線垂直數量積為零列出方程組求出法向量;(4)將空間位置關系轉化為向量關系;(5)根據定理結論求出相應的角和距離.
【題型】解答題
【結束】
22
【題目】已知橢圓![]() 的短軸長為2,且橢圓
的短軸長為2,且橢圓![]() 過點
過點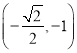 .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設直線![]() 過定點
過定點![]() ,且斜率為
,且斜率為![]() ,若橢圓
,若橢圓![]() 上存在
上存在![]() 兩點關于直線
兩點關于直線![]() 對稱,
對稱, ![]() 為坐標原點,求
為坐標原點,求![]() 的取值范圍及
的取值范圍及![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某機構在某一學校隨機抽取30名學生參加環保知識測試,測試成績(單位:分)如圖所示,假設得分值的中位數為me , 眾數為m0 , 平均值為 ![]() ,則( )
,則( ) 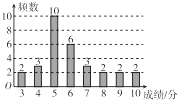
A.me=m0= ![]()
B.me=m0< ![]()
C.me<m0< ![]()
D.m0<me< ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com