
【題目】已知橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() ,過
,過![]() 作垂直于
作垂直于![]() 軸的直線
軸的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,且滿足
兩點,且滿足![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)過![]() 作斜率為
作斜率為![]() 的直線
的直線![]() 交
交![]() 于
于![]() 兩點.
兩點. ![]() 為坐標原點,若
為坐標原點,若![]() 的面積為
的面積為![]() ,求橢圓
,求橢圓![]() 的方程.
的方程.
科目:高中數學 來源: 題型:
【題目】為增強市民的節能環保意識,鄭州市面向全市征召義務宣傳志愿者,從符合條件的500名志愿者中隨機抽取100名,其年齡頻率分布直方圖如圖所示,其中年齡分組區是:![]() .
.
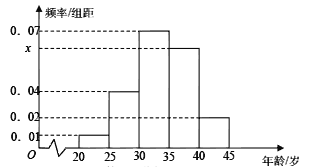
(Ⅰ)求圖中![]() 的值,并根據頻率分布直方圖估計這500名志愿者中年齡在
的值,并根據頻率分布直方圖估計這500名志愿者中年齡在![]() 歲的人數;
歲的人數;
(Ⅱ)在抽出的100名志愿者中按年齡采用分層抽樣的方法抽取10名參加中心廣場的宣傳活動,再從這10名志愿者中選取3名擔任主要負責人.記這3名志愿者中“年齡低于35歲”的人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在邊長為1的等邊三角形ABC中,D,E分別是AB,AC邊上的點,AD=AE,F是BC的中點,AF與DE交于點G,將△ABF沿AF折起,得到如圖2所示的三棱錐A﹣BCF,其中BC=![]() .
.
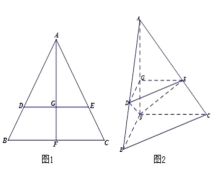
(Ⅰ)證明:DE∥平面BCF;
(Ⅱ)證明:CF⊥平面ABF;
(Ⅲ)當AD=![]() 時,求三棱錐F﹣DEG的體積.
時,求三棱錐F﹣DEG的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知國家某5A級大型景區對擁擠等級與每日游客數量![]() (單位:百人)的關系有如下規定:當
(單位:百人)的關系有如下規定:當![]()
![]() 時,擁擠等級為“優”;當
時,擁擠等級為“優”;當![]()
![]() 時,擁擠等級為“良”;當
時,擁擠等級為“良”;當![]()
![]() 時,擁擠等級為“擁擠”;當
時,擁擠等級為“擁擠”;當![]()
![]() 時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
時,擁擠等級為“嚴重擁擠”。該景區對6月份的游客數量作出如圖的統計數據:
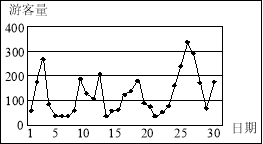
(Ⅰ)下面是根據統計數據得到的頻率分布表,求出![]() 的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
的值,并估計該景區6月份游客人數的平均值(同一組中的數據用該組區間的中點值作代表);
游客數量 (單位:百人) |
|
|
|
|
天數 |
|
|
|
|
頻率 |
|
|
|
|
(Ⅱ)某人選擇在6月1日至6月5日這5天中任選2天到該景區游玩,求他這2天遇到的游客擁擠等級均為“優”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知過點![]() 的直線
的直線![]() 的參數方程是
的參數方程是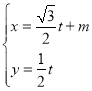 (
(![]() 為參數).以平面直角坐標系的原點為極點,
為參數).以平面直角坐標系的原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,曲線
軸的正半軸為極軸,建立極坐標系,曲線![]() 的極坐標方程式為
的極坐標方程式為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=si n![]() -2cos2
-2cos2![]() +1.
+1.
(1)求f(x)的最小正周期;
(2)若函數y=f(x)與y=g(x)的圖象關于直線x=1對稱,求當x∈![]() 時,y=g(x)的最大值.
時,y=g(x)的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在坐標原點![]() 的橢圓
的橢圓![]() 經過點
經過點![]() ,且點
,且點![]() 為其右焦點.
為其右焦點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)是否存在平行于![]() 的直線
的直線![]() ,使得直線
,使得直線![]() 與橢圓
與橢圓![]() 有公共點,且直線
有公共點,且直線![]() 與
與![]() 的距離等于4?若存在,求出直線
的距離等于4?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數);在以原點
為參數);在以原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(I)求曲線![]() 的極坐標方程和曲線
的極坐標方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(II)若射線![]() 與曲線
與曲線![]() ,
,![]() 的交點分別為
的交點分別為![]() (
(![]() 異于原點),當斜率
異于原點),當斜率![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了迎接世博會,某旅游區提倡低碳生活,在景區提供自行車出租.該景區有50輛自行車供游客租賃使用,管理這些自行車的費用是每日115元.根據經驗,若每輛自行車的日租金不超過6元,則自行車可以全部租出;若超出6元,則每超過1元,租不出的自行車就增加3輛.為了便于結算,每輛自行車的日租金![]() (元)只取整數,并且要求出租自行車一日的總收入必須高于這一日的管理費用,用
(元)只取整數,并且要求出租自行車一日的總收入必須高于這一日的管理費用,用![]() (元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費用后的所得)。
(元)表示出租自行車的日凈收入(即一日中出租自行車的總收入減去管理費用后的所得)。
(1)求函數![]() 的解析式及其定義域;
的解析式及其定義域;
(2)試問當每輛自行車的日租金定為多少元時,才能使一日的凈收入最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com