
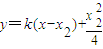 (k>0),與曲線方程聯立,則得
(k>0),與曲線方程聯立,則得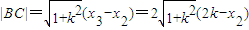 ,,同理
,,同理 ,根據|AB|=|BC|,可得函數關系式;
,根據|AB|=|BC|,可得函數關系式;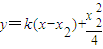 (k>0),
(k>0),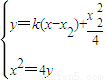 消y得x2-4kx-x22+4kx2=0,
消y得x2-4kx-x22+4kx2=0,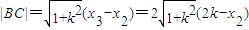 ,(7分)
,(7分)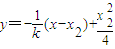 ,
,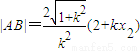 ,(9分)
,(9分)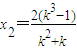 ,(11分)
,(11分) (k>0). (13分)
(k>0). (13分)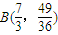 ,
,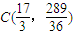 ,
,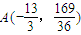 ,所以
,所以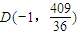 . (18分)
. (18分)

科目:高中數學 來源: 題型:
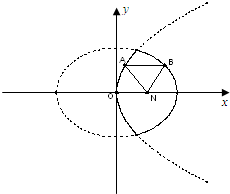 [理]如圖,已知動點A,B分別在圖中拋物線y2=4x及橢圓
[理]如圖,已知動點A,B分別在圖中拋物線y2=4x及橢圓| x2 |
| 4 |
| y2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:盧灣區二模 題型:解答題
查看答案和解析>>
科目:高中數學 來源:2010-2011學年江蘇省鹽城中學高二(上)期末數學試卷(解析版) 題型:填空題
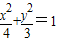 的實線上運動,若AB∥x軸,點N的坐標為(1,0),則△ABN的周長l的取值范圍是 .
的實線上運動,若AB∥x軸,點N的坐標為(1,0),則△ABN的周長l的取值范圍是 .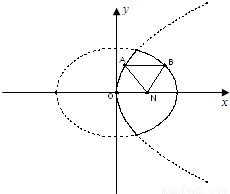
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com