設函數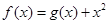
，曲線
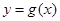在點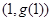
處的切線方程為
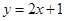，則曲線
在點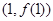
處切線的斜率為
4
解析試題分析：先根據曲線y=g（x）在點（1，g（1））處的切線方程為y=2x+1，可得g′（1）=2，再利用函數f（x）=g（x）+x2，可知f′（x）=g′（x）+2x，從而可求曲線y=f（x）在點（1，f（1））處切線的斜率．解：由題意，∵曲線y=g（x）在點（1，g（1））處的切線方程為y=2x+1，∴g′（1）=2，∵函數f（x）=g（x）+x2，∴f′（x）=g′（x）+2x∴f′（1）=g′（1）+2∴f′（1）=2+2=4∴曲線y=f（x）在點（1，f（1））處切線的斜率為4，故答案為：4
考點：導數的幾何意義
點評：本題考查的重點是曲線在點處切線的斜率，解題的關鍵是利用導數的幾何意義．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
(單位：
)的作用下沿與力
相同的方向,從
處運動到
(單位：
)處,則力
做的功為 焦．
和直線
，
及
軸所圍圖形的面積為 .
且
，則實數
的值等于 ； 
在
內有極小值，則實數
的取值范圍 
.若曲線
與直線
所圍成封閉圖形的面積為
，則
.
上的點
的切線方程為________________。
-x+3在點（1，3）處的切線方程為