
【題目】質檢部門從某超市銷售的甲、乙兩種食用油中分別隨機抽取100桶檢測某項質量指標,由檢測結果得到如圖的頻率分布直方圖:
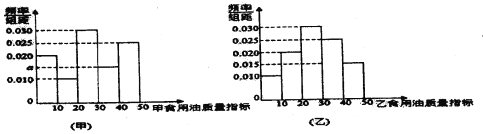
(I)寫出頻率分布直方圖(甲)中![]() 的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為
的值;記甲、乙兩種食用油100桶樣本的質量指標的方差分別為![]() ,試比較
,試比較![]() 的大小(只要求寫出答案);
的大小(只要求寫出答案);
(Ⅱ)佑計在甲、乙兩種食用油中各隨機抽取1桶,恰有一個桶的質量指標大于20,且另—個桶的質量指標不大于20的概率;
(Ⅲ)由頻率分布直方圖可以認為,乙種食用油的質量指標值![]() 服從正態分布
服從正態分布![]() .其中
.其中![]() 近似為樣本平均數
近似為樣本平均數![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() ,設
,設![]() 表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55, 38.45)的桶數,求
表示從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55, 38.45)的桶數,求![]() 的數學期望.
的數學期望.
注:①同一組數據用該區間的中點值作代表,計算得![]() :
:
②若![]() ,則
,則![]() ,
,![]() .
.
【答案】(1)![]() ;(2)0.42;(3)6.826.
;(2)0.42;(3)6.826.
【解析】
(Ⅰ)由頻率分布直方圖的矩形面積和為1可得![]() 再由分布的離散程度即可比較方差大小;
再由分布的離散程度即可比較方差大小;
(Ⅱ)設事件A,事件B,事件C,求出P(A),P(B),P(C)即可;
(Ⅲ)求出從乙種食用油中隨機抽取10桶,其質量指標值位于(14.55,38.45)的概率是0.6826,得到X~B(10,0.6826),求出EX即可.
(Ⅰ) ![]() ;
;
(Ⅱ)設事件![]() :在甲公司產品中隨機抽取1顆,其質量指標不大于20,
:在甲公司產品中隨機抽取1顆,其質量指標不大于20,
事件![]() :在乙公司產品中隨機抽取1顆,其質量指標不大于20,
:在乙公司產品中隨機抽取1顆,其質量指標不大于20,
事件![]() :在甲、乙公司產品中隨機抽各取1顆,恰有一顆糖果的質量指標大于20,且另一個不大于20,則
:在甲、乙公司產品中隨機抽各取1顆,恰有一顆糖果的質量指標大于20,且另一個不大于20,則![]() ,
,![]() ,
,
![]()
![]() ;
;
(Ⅲ)計算得: ![]() ,由條件得
,由條件得![]()
從而![]()
![]() ,
,
![]() 從乙公司產品中隨機抽取10顆,其質量指標值位于(14.55,38.45)的概率是0.6826,
從乙公司產品中隨機抽取10顆,其質量指標值位于(14.55,38.45)的概率是0.6826,
依題意得![]() ,
,
![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】過拋物線![]() :
:![]() 的焦點
的焦點![]() 的直線
的直線![]() (傾斜角為銳角)交拋物線于
(傾斜角為銳角)交拋物線于![]() ,
,![]() 兩點,若
兩點,若![]() 為線段
為線段![]() 的中點,連接
的中點,連接![]() 并延長交拋物線
并延長交拋物線![]() 于點
于點![]() ,已知
,已知![]() ,則直線
,則直線![]() 的斜率是( )
的斜率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面幾種推理過程是演繹推理的是( )
A. 某校高三有8個班,1班有51人,2班有53人,3班有52人,由此推測各班人數都超過50人
B. 由三角形的性質,推測空間四面體的性質
C. 平行四邊形的對角線互相平分,菱形是平行四邊形,所以菱形的對角線互相平分
D. 在數列![]() 中,
中,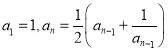 ,可得
,可得![]() ,由此歸納出
,由此歸納出![]() 的通項公式
的通項公式![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】f(x)是定義在(0,+∞)上的單調增函數,滿足f(xy)=f(x)+f(y),f(3)=1,當f(x)+f(x-8)≤2時,x的取值范圍是( )
A.(8,+∞)B.(8,9]C.[8,9]D.(0,8)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是函數
是函數![]() 定義域的一個子集,若存在
定義域的一個子集,若存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 是
是![]() 的一個“準不動點”,也稱
的一個“準不動點”,也稱![]() 在區間
在區間![]() 上存在準不動點,已知
上存在準不動點,已知![]() ,
,![]() .
.
(1)若![]() ,求函數
,求函數![]() 的準不動點;
的準不動點;
(2)若函數![]() 在區間
在區間![]() 上存在準不動點,求實數
上存在準不動點,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ;
;
(1)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(2)若定義在![]() 上奇函數
上奇函數![]() 滿足
滿足![]() ,且當
,且當![]() 時,
時, ![]() ,
,
求![]() 在
在![]() 上的反函數
上的反函數![]() ;
;
(3)對于(2)中的![]() ,若關于
,若關于![]() 的不等式
的不等式 在
在![]() 上恒成立,求實
上恒成立,求實
數![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】類比平面內正三角形的“三邊相等,三內角相等”的性質,可推出正四面體的下列性質,你認為比較恰當的是( )
①各棱長相等,同一頂點上的任兩條棱的夾角都相等;
②各個面都是全等的正三角形,相鄰兩個面所成的二面角都相等;
③各面都是面積相等的三角形,同一頂點上的任兩條棱的夾角都相等.
A. ①B. ②C. ①②③D. ③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com