【題目】地為綠化環(huán)境，移栽了銀杏樹
棵，梧桐樹
棵.它們移栽后的成活率分別
為
、
，每棵樹是否存活互不影響，在移栽的
棵樹中：
（1）求銀杏樹都成活且梧桐樹成活
棵的概率；
（2）求成活的棵樹
的分布列與期望.
智能訓(xùn)練練測考系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
【題目】某地隨著經(jīng)濟(jì)的發(fā)展，居民收入逐年增長，下表是該地一建設(shè)銀行連續(xù)五年的儲蓄存款（年底余額），如下表1：
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款y（千億元） | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便，工作人員將上表的數(shù)據(jù)進(jìn)行了處理， 
得到下表2：
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
（Ⅰ）求z關(guān)于t的線性回歸方程；
（Ⅱ）通過（Ⅰ）中的方程，求出y關(guān)于x的回歸方程；
（Ⅲ）用所求回歸方程預(yù)測到2020年年底，該地儲蓄存款額可達(dá)多少？
（附：對于線性回歸方程
，其中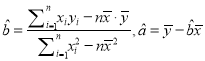
）
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)
為坐標(biāo)原點(diǎn)，動點(diǎn)
在橢圓
上，過
作
軸的垂線，垂足為
，點(diǎn)
滿足
.（Ⅰ）求點(diǎn)
的軌跡方程
；
（Ⅱ）過
的直線
與點(diǎn)
的軌跡交于
兩點(diǎn)，過
作與
垂直的直線
與點(diǎn)
的軌跡交于
兩點(diǎn)，求證： 
為定值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】設(shè)圓
的圓心為
，直線
過點(diǎn)
且與
軸不重合， 
交圓
于
兩點(diǎn)，過
作
的平行線交
于點(diǎn)
.
（1）證明
為定值，并寫出點(diǎn)
的軌跡方程；
（2）設(shè)
，過點(diǎn)
作直線
，交點(diǎn)
的軌跡于
兩點(diǎn) (異于
),直線
的斜率分別為
，證明： 
為定值.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】“累積凈化量（
）”是空氣凈化器質(zhì)量的一個重要衡量指標(biāo)，它是指空氣凈化器從開始使用到凈化效率為
時對顆粒物的累積凈化量，以克表示.根據(jù)
《空氣凈化器》國家標(biāo)準(zhǔn)，對空氣凈化器的累計凈化量（
）有如下等級劃分：
累積凈化量（克） |
|
|
| 12以上 |
等級 |
|
|
|
|
為了了解一批空氣凈化器（共2000臺）的質(zhì)量，隨機(jī)抽取
臺機(jī)器作為樣本進(jìn)行估計，已知這
臺機(jī)器的累積凈化量都分布在區(qū)間
中.按照
均勻分組，其中累積凈化量在
的所有數(shù)據(jù)有： 
和
，并繪制了如下頻率分布直方圖：
（1）求
的值及頻率分布直方圖中的
值；
（2）以樣本估計總體，試估計這批空氣凈化器（共2000臺）中等級為
的空氣凈化器有多少臺？
（3）從累積凈化量在
的樣本中隨機(jī)抽取2臺，求恰好有1臺等級為
的概率.
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知曲線
， 
，則下列說法正確的是（ ）
A. 把
上各點(diǎn)橫坐標(biāo)伸長到原來的2倍，縱坐標(biāo)不變，再把得到的曲線向右平移
個單位長度，得到曲線
B. 把
上各點(diǎn)橫坐標(biāo)伸長到原來的2倍，縱坐標(biāo)不變，再把得到的曲線向右平移
個單位長度，得到曲線
C. 把曲線
向右平移
個單位長度，再把得到的曲線上各點(diǎn)橫坐標(biāo)縮短到原來的
，縱坐標(biāo)不變，得到曲線
D. 把曲線
向右平移
個單位長度，再把得到的曲線上各點(diǎn)橫坐標(biāo)縮短到原來的
，縱坐標(biāo)不變，得到曲線
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】已知橢圓
的左焦點(diǎn)
與拋物線
的焦點(diǎn)重合，橢圓
的離心率為
，過點(diǎn)
作斜率不為0的直線
，交橢圓
于
兩點(diǎn)，點(diǎn)
，且
為定值．
（1）求橢圓
的方程；
（2）求
面積的最大值．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
【題目】如圖，在底面是菱形的四棱錐
中, 
平面
， 
，點(diǎn)
分別為
的中點(diǎn)，設(shè)直線
與平面
交于點(diǎn)
.
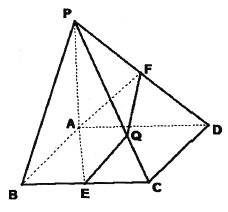
（1）已知平面
平面
，求證： 
.
（2）求直線
與平面
所成角的正弦值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
