
【題目】已知函數f(x)=tan![]() .
.
(1)求f(x)的定義域與最小正周期;
(2)設α∈![]() ,若f
,若f![]() =2cos 2α,求α的大小.
=2cos 2α,求α的大小.
【答案】(1)![]() x∈R
x∈R![]() x≠
x≠![]() ,k∈Z
,k∈Z![]() ,
,![]() (2)α=
(2)α=![]() .
.
【解析】
(1)根據正切函數性質求定義域與最小正周期; (2)代入,根據兩角和正切公式以及二倍角余弦公式化簡等式為sin 2α=![]() .再根據角范圍求結果.
.再根據角范圍求結果.
(1)由2x+![]() +kπ,k∈Z,得x≠
+kπ,k∈Z,得x≠![]() ,k∈Z,
,k∈Z,
所以f(x)的定義域為![]() x∈R
x∈R![]() x≠
x≠![]() ,k∈Z
,k∈Z![]() .
.
f(x)的最小正周期為![]() .
.
(2)由f![]() =2cos 2α,得tan
=2cos 2α,得tan![]() =2cos 2α,
=2cos 2α,
即 =2(cos2α-sin2α),
=2(cos2α-sin2α),
整理得![]() =2(cos α+sin α)(cos α-sin α).
=2(cos α+sin α)(cos α-sin α).
因為α∈![]() ,所以sin α+cos α≠0.
,所以sin α+cos α≠0.
因此(cos α-sin α)2=![]() ,即sin 2α=
,即sin 2α=![]() .
.
由α∈![]() ,得2α∈
,得2α∈![]() ,所以2α=
,所以2α=![]() ,即α=
,即α=![]() .
.


科目:高中數學 來源: 題型:
【題目】某高中生調查了當地某小區的50戶居民由于臺風造成的經濟損失,將收集的數據分成![]() 三組,并作出如下頻率分布直方圖:
三組,并作出如下頻率分布直方圖:

(1)在直方圖的經濟損失分組中,以各組的區間中點值代表該組的各個值,并以經濟損失落入該區間的頻率作為經濟損失取該區間中點值的概率(例如:經濟損失![]() 則取
則取![]() ,且
,且![]() 的概率等于經濟損失落入
的概率等于經濟損失落入![]() 的頻率)。現從當地的居民中隨機抽出2戶進行捐款援助,設抽出的2戶的經濟損失的和為
的頻率)。現從當地的居民中隨機抽出2戶進行捐款援助,設抽出的2戶的經濟損失的和為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
(2)臺風后居委會號召小區居民為臺風重災區捐款,此高中生調查的50戶居民捐款情況如下表,在表格空白處填寫正確數字,并說明是否有95%以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
經濟損失不超過4000元 | 經濟損失超過4000元 | 合計 | |
捐款超過500元 | 30 | ||
捐款不超過500元 | 6 | ||
合計 |
附:臨界值表參考公式:  .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD的中心為O , 四邊形OBEF為矩形,平面OBEF⊥平面ABCD , 點G為AB的中點,AB=BE=2.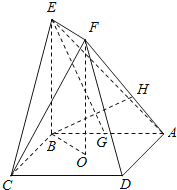
(1)求證:EG∥平面ADF;
(2)求二面角O-EF-C的正弦值;
(3)設H為線段AF上的點,且AH= ![]() HF , 求直線BH和平面CEF所成角的正弦值.
HF , 求直線BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若將函數y=2sin 2x的圖像向左平移 ![]() 個單位長度,則評議后圖象的對稱軸為( )
個單位長度,則評議后圖象的對稱軸為( )
A.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() –
– ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某險種的基本保費為a(單位:元),繼續購買該險種的投保人稱為續保人,續保人的本年度的保費與其上年度的出險次數的關聯如下:
上年度出險次數 | 0 | 1 | 2 | 3 | 4 |
|
保費 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
設該險種一續保人一年內出險次數與相應概率如下:
一年內出險次數 | 0 | 1 | 2 | 3 | 4 |
|
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0. 05 |
(1)求一續保人本年度的保費高于基本保費的概率;
(2)若一續保人本年度的保費高于基本保費,求其保費比基本保費高出60%的概率;
(3)求續保人本年度的平均保費與基本保費的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E: ![]() 的焦點在
的焦點在 ![]() 軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
軸上,A是E的左頂點,斜率為k(k>0)的直線交E于A,M兩點,點N在E上,MA⊥NA.
(1)當t=4, ![]() 時,求△AMN的面積;
時,求△AMN的面積;
(2)當 ![]() 時,求k的取值范圍.
時,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】A、B、C三個班共有100名學生,為調查他們的體育鍛煉情況,通過分層抽樣獲得了部分學生一周的鍛煉時間,數據如下表(單位:小時);
A班 | 6 6.5 7 7.5 8 |
B班 | 6 7 8 9 10 11 12 |
C班 | 3 4.5 6 7.5 9 10.5 12 13.5 |
(1)試估計C班的學生人數;
(2)從A班和C班抽出的學生中,各隨機選取一人,A班選出的人記為甲,C班選出的人記為乙,假設所有學生的鍛煉時間相對獨立,求該周甲的鍛煉時間比乙的鍛煉時間長的概率;
(3)再從A、B、C三個班中各隨機抽取一名學生,他們該周的鍛煉時間分別是7,9,8.25(單位:小時),這3個新數據與表格中的數據構成的新樣本的平均數記 ![]() ,表格中數據的平均數記為
,表格中數據的平均數記為 ![]() ,試判斷
,試判斷 ![]() 和
和 ![]() 的大小,(結論不要求證明)
的大小,(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(Ⅰ)求數列{bn}的通項公式;
(Ⅱ)數列{bn}的前n項和為Sn,求證:數列{Sn+![]() }是等比數列.
}是等比數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com