【題目】對任意實數
給出下列命題:①“
”是“
”的充要條件;②“
是無理數”是“
是無理數”的充要條件;③“
”是“
”的充分條件;④“
”是“
”的必要條件.其中真命題的個數是( )
A.1B.2C.3D.4
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如圖是一“T”型水渠的平面視圖（俯視圖），水渠的南北方向和東西方向軸截面均為矩形，南北向渠寬為4m，東西向渠寬
m（從拐角處，即圖中
，
處開始）．假定渠內的水面始終保持水平位置（即無高度差）．
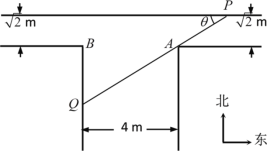
（1）在水平面內，過點的一條直線與水渠的內壁交于
，
兩點，且與水渠的一邊的夾角為
，將線段
的長度
表示為
的函數；
（2）若從南面漂來一根長為7m的筆直的竹竿（粗細不計），竹竿始終浮于水平面內，且不發生形變，問：這根竹竿能否從拐角處一直漂向東西向的水渠（不會卡住）？請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校的一個社會實踐調查小組，在對該校學生的良好“用眼習慣”的調查中，隨機發放了120分問卷.對收回的100份有效問卷進行統計，得到如
下列聯表：
做不到科學用眼 | 能做到科學用眼 | 合計 | |
男 | 45 | 10 | 55 |
女 | 30 | 15 | 45 |
合計 | 75 | 25 | 100 |
（1）現按女生是否能做到科學用眼進行分層，從45份女生問卷中抽取了6份問卷，從這6份問卷中再隨機抽取3份，并記其中能做到科學用眼的問卷的份數
，試求隨機變量的分布列和數學期望；
（2）若在犯錯誤的概率不超過
的前提下認為良好“用眼習慣”與性別有關，那么根據臨界值表，最精確的的值應為多少？請說明理由.
附：獨立性檢驗統計量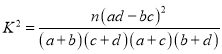
，其中
.
獨立性檢驗臨界值表：
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.840 | 5.024 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某中學某社團為研究高三學生課下鉆研數學時間與數學考試中的解答題得分的關系，隨機調查了某中學高三某班
名學生每周課下鉆研數學時間
(單位：小時)與高三下學期期中考試數學解答題得分
，數據如下表：
| 2 | 4 | 6 | 8 | 10 | 12 |
| 30 | 38 | 44 | 48 | 50 | 54 |
（1）根據上述數據，求出數學考試中的解答題得分與該學生課下鉆研數學時間的線性回歸方程，并預測某學生每周課下鉆研數學時間為
小時其數學考試中的解答題得分；
（2）從這人中任選
人，求人中至少有
人課下鉆研數學時間不低于
小時的概率.
參考公式：
，其中
，
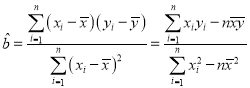；參考數據：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知8支球隊中有3支弱隊，以抽簽方式將這8支球隊分為A、B兩組，每組4支．求：（1）A、B兩組中有一組恰有兩支弱隊的概率；
（2）A組中至少有兩支弱隊的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某運輸公司每天至少向某地運送
物質，該公司有8輛載重為
的
型卡車與4輛載重為
的
型卡車，有10名駕駛員，每輛卡車每天往返的次數為型卡車4次，型卡車3次；每輛卡車每天往返的成本為型卡車320元，型卡車504元，你認為該公司怎樣調配車輛，使運費成本最低，最低運費是多少？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人各射擊一次，擊中目標的概率分別是
和
，假設兩人射擊是否擊中目標，相互之間沒有影響；每次射擊是否擊中目標，相互之間沒有影響．
（1）求甲射擊4次，至多1次未擊中目標的概率；
（2）求兩人各射擊4次，甲恰好擊中目標2次且乙恰好擊中目標3次的概率；
（3）假設某人連續2次未擊中目標，則停止射擊，求乙恰好射擊5次后被中止射擊的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】有4位同學在同一天的上午、下午參加“身高與體重”“立定跳遠”“肺活量”“握力”“臺階”5個項目的測試，每位同學上午、下午各測試1個項目，且不重復.若上午不測“握力”項目，下午不測“臺階”項目，其余項目上午、下午都各測試1人，則不同的安排方式有多少種？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
