
【題目】給出下列五個命題:
①凈![]() 三種個體按
三種個體按![]() 的比例分層抽樣調查,如果抽取的
的比例分層抽樣調查,如果抽取的![]() 個體為9個,則樣本容易為30;②一組數據1、2、3、4、5的平均數、眾數、中位數相同;③甲組數據的方差為5,乙組數據為5、6、9、10、5,那么這兩組數據中較穩定的是甲;④已知具有線性相關關系的兩個變量滿足的回歸直線方程為
個體為9個,則樣本容易為30;②一組數據1、2、3、4、5的平均數、眾數、中位數相同;③甲組數據的方差為5,乙組數據為5、6、9、10、5,那么這兩組數據中較穩定的是甲;④已知具有線性相關關系的兩個變量滿足的回歸直線方程為![]() .則
.則![]() 每增加1個單位,
每增加1個單位,![]() 平均減少2個單位;⑤統計的10個樣本數據為125,120,122,105,130,114,116,95,120,134,則樣本數據落在
平均減少2個單位;⑤統計的10個樣本數據為125,120,122,105,130,114,116,95,120,134,則樣本數據落在![]() 內的頻率為0.4其中真命題為( )
內的頻率為0.4其中真命題為( )
A. ①②④B. ②④⑤C. ②③④D. ③④⑤
【答案】B
【解析】
由題意①中,根據分層抽樣的方法,即可求解是錯誤的;②中,利用平均數、眾數、中位數的公式求解,即可得到判斷;③中,利用平均數和方差的公式,即可得到判斷;④中,根據回歸系數的含義,即可得到判斷;⑤中,根據古典概型的概率計算公式,即可求解,作出判斷.
,
①樣本容量為9÷![]() =18,①是假命題;②數據1,2,3,3,4,5的平均數為
=18,①是假命題;②數據1,2,3,3,4,5的平均數為![]() ×(1+2+3+3+4+5)=3,中位數為3,眾數為3,都相同,②是真命題;③
×(1+2+3+3+4+5)=3,中位數為3,眾數為3,都相同,②是真命題;③![]() 乙=
乙=![]() =7,s
=7,s![]() =
=![]() ×[(5-7)2+(6-7)2+(9-7)2+(10-7)2+(5-7)2]=
×[(5-7)2+(6-7)2+(9-7)2+(10-7)2+(5-7)2]=![]() ×(4+1+4+9+4)=4.4,∴s
×(4+1+4+9+4)=4.4,∴s![]() >s
>s![]() ,∴乙穩定,③是假命題;④是真命題;⑤數據落在[114.5,124.5)內的有120,122,116,120,共4個,故其頻率為0.4,⑤是真命題.
,∴乙穩定,③是假命題;④是真命題;⑤數據落在[114.5,124.5)內的有120,122,116,120,共4個,故其頻率為0.4,⑤是真命題.


科目:高中數學 來源: 題型:
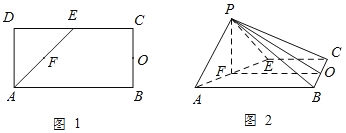
【題目】如圖1,在矩形ABCD中,AB=4,AD=2,E,F,O分別為DC,AE,BC的中點.以AE為折痕把△ADE折起,使點D到達點P的位置,且平面PAE⊥平面ABCE(如圖2).
(Ⅰ)求證:BC⊥平面POF;
(Ⅱ)求直線PA與平面PBC所成角的正弦值;
(Ⅲ)在線段PE上是否存在點M,使得AM∥平面PBC?若存在,求![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
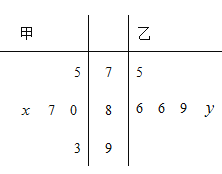
【題目】在學校組織的英語單詞背誦比賽中,5位評委對甲、乙兩名同學的評分如莖葉圖所示(分數為整數,且滿分100分),若甲同學所得評分的中位數為87,乙同學所得評分的唯一眾數為86,則甲同學所得評分的平均數不小于乙同學所得評分的平均數的概率為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大型工廠有![]() 臺大型機器,在
臺大型機器,在![]() 個月中,
個月中,![]() 臺機器至多出現
臺機器至多出現![]() 次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需
次故障,且每臺機器是否出現故障是相互獨立的,出現故障時需![]() 名工人進行維修.每臺機器出現故障的概率為
名工人進行維修.每臺機器出現故障的概率為![]() .已知
.已知![]() 名工人每月只有維修
名工人每月只有維修![]() 臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得
臺機器的能力,每臺機器不出現故障或出現故障時有工人維修,就能使該廠獲得![]() 萬元的利潤,否則將虧損
萬元的利潤,否則將虧損![]() 萬元.該工廠每月需支付給每名維修工人
萬元.該工廠每月需支付給每名維修工人![]() 萬元的工資.
萬元的工資.
(1)若每臺機器在當月不出現故障或出現故障時有工人進行維修,則稱工廠能正常運行.若該廠只有![]() 名維修工人,求工廠每月能正常運行的概率;
名維修工人,求工廠每月能正常運行的概率;
(2)已知該廠現有![]() 名維修工人.
名維修工人.
(ⅰ)記該廠每月獲利為![]() 萬元,求
萬元,求![]() 的分布列與數學期望;
的分布列與數學期望;
(ⅱ)以工廠每月獲利的數學期望為決策依據,試問該廠是否應再招聘![]() 名維修工人?
名維修工人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列有關命題的說法錯誤的是( )
A.若“p∨q”為假命題,則p,q均為假命題
B.“x=1”是“x≥1”的充分不必要條件
C.“sinx=![]() ”的必要不充分條件是“x=
”的必要不充分條件是“x=![]() ”
”
D.若命題p:x0∈R,x02≥0,則命題¬p:x∈R,x2<0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的個數是( )
①一組數據的標準差越大,則說明這組數據越集中;
②曲線![]() 與曲線
與曲線![]() 的焦距相等;
的焦距相等;
③在頻率分布直方圖中,估計的中位數左邊和右邊的直方圖的面積相等;
④已知橢圓![]() ,過點
,過點![]() 作直線,當直線斜率為
作直線,當直線斜率為![]() 時,M剛好是直線被橢圓截得的弦AB的中點.
時,M剛好是直線被橢圓截得的弦AB的中點.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究高中學生對鄉村音樂的態度(喜歡和不喜歡兩種態度)與性別的關系,運用2×2列聯表進行獨立性檢驗,經計算K2=8.01,附表如下:
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
參照附表,得到的正確的結論是( )
A. 有99%以上的把握認為“喜歡鄉村音樂與性別有關”
B. 有99%以上的把握認為“喜歡鄉村音樂與性別無關”
C. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別有關”
D. 在犯錯誤的概率不超過0.1%的前提下,認為“喜歡鄉村音樂與性別無關”
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() ,
,![]() 為曲線
為曲線![]() 上的一動點.
上的一動點.
(I)求動點![]() 對應的參數從
對應的參數從![]() 變動到
變動到![]() 時,線段
時,線段![]() 所掃過的圖形面積;
所掃過的圖形面積;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 的另一個交點為
的另一個交點為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 為線段
為線段![]() 的中點?若存在,求出點
的中點?若存在,求出點![]() 坐標;若不存在,說明理由.
坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com