
(本小題滿分12分)
在 中,
中,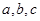 分別為內(nèi)角
分別為內(nèi)角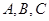 的對(duì)邊,且
的對(duì)邊,且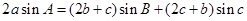 .
.
(1)求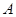
 的大小;
的大小;
(2)若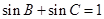 ,試判斷
,試判斷 的形狀;
的形狀;
(1) 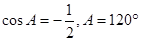 . (2)
. (2)  是等腰的鈍角三角形.
是等腰的鈍角三角形.
解析試題分析:(Ⅰ)利用正弦定理把題設(shè)等式中的角的正弦轉(zhuǎn)化成邊,求得a,b和c關(guān)系式,代入余弦定理中求得cosA的值,進(jìn)而求得A.
(Ⅱ)把(Ⅰ)中a,b和c關(guān)系式利用正弦定理轉(zhuǎn)化成角的正弦,與sinB+sinC=1聯(lián)立求得sinB和sinC的值,進(jìn)而根據(jù)C,B的范圍推斷出B=C,可知△ABC是等腰的鈍角三角形
(1)由已知,根據(jù)正弦定理得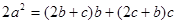 ,
,
即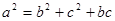 .
.
由余弦定理得 ,
,
故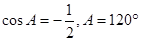 .……6分
.……6分
(2)由(1)得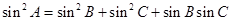 .
.
又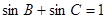 ,得
,得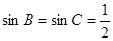 .
.
因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/4f/9/eiwan3.png" style="vertical-align:middle;" />,
故B=C.
所以 是等腰的鈍角三角形. …………12分考點(diǎn):本題主要考查正弦定理和余弦定理的應(yīng)用.
是等腰的鈍角三角形. …………12分考點(diǎn):本題主要考查正弦定理和余弦定理的應(yīng)用.
點(diǎn)評(píng):解決該試題的關(guān)鍵是在解三角形問題中一般借助正弦定理和余弦定理邊化角,角化邊達(dá)到解題的目的.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
為了豎一塊廣告牌,要制造三角型支架,三角形支架如圖所示,要求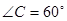 ,
,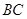 長(zhǎng)度大于
長(zhǎng)度大于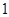 米,且
米,且 比
比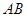 長(zhǎng)
長(zhǎng)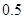 米,為了廣告牌的穩(wěn)固,要求
米,為了廣告牌的穩(wěn)固,要求 的長(zhǎng)度越短越好,求
的長(zhǎng)度越短越好,求 最短為多少?
最短為多少?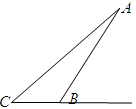
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13 分)
據(jù)氣象部門預(yù)報(bào),在距離某碼頭南偏東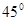 方向600km處的熱帶風(fēng)暴中心,正以每小時(shí)20km的速度向正北方向移動(dòng),距風(fēng)暴中心450km以內(nèi)的地區(qū)都將受到影響,從現(xiàn)在起多長(zhǎng)時(shí)間后,該碼頭將受到熱帶風(fēng)暴中心的影響,影響多長(zhǎng)時(shí)間?(精確到0.1h)
方向600km處的熱帶風(fēng)暴中心,正以每小時(shí)20km的速度向正北方向移動(dòng),距風(fēng)暴中心450km以內(nèi)的地區(qū)都將受到影響,從現(xiàn)在起多長(zhǎng)時(shí)間后,該碼頭將受到熱帶風(fēng)暴中心的影響,影響多長(zhǎng)時(shí)間?(精確到0.1h)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分13分)我炮兵陣地位于地面A處,兩觀察所分別位于地面點(diǎn)C和D處,已知CD=6 ,∠ACD=45°,∠ADC=75°, 目標(biāo)出現(xiàn)于地面點(diǎn)B處時(shí),測(cè)得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標(biāo)的距離.
,∠ACD=45°,∠ADC=75°, 目標(biāo)出現(xiàn)于地面點(diǎn)B處時(shí),測(cè)得∠BCD=30°,∠BDC=15°(如圖),求炮兵陣地到目標(biāo)的距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
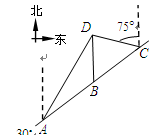
如圖,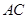 是佛山市一環(huán)東線的一段,其中
是佛山市一環(huán)東線的一段,其中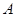 、
、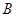 、
、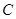 分別是林上路、佛陳路、花卉大道出口,經(jīng)測(cè)量陳村花卉世界
分別是林上路、佛陳路、花卉大道出口,經(jīng)測(cè)量陳村花卉世界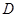 位于點(diǎn)
位于點(diǎn)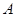 的北偏東
的北偏東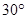 方向
方向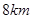 處,位于點(diǎn)
處,位于點(diǎn)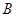 的正北方向,位于點(diǎn)
的正北方向,位于點(diǎn)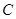 的北偏西
的北偏西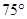 方向上,并且
方向上,并且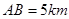 .
.
(1) 求佛陳路出口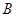 與花卉世界
與花卉世界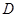 之間的距離;(精確到0.1km)
之間的距離;(精確到0.1km)
(2) 求花卉大道出口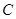 與花卉世界
與花卉世界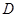 之間的距離.(精確到0.1km)
之間的距離.(精確到0.1km)
(參考數(shù)據(jù):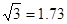 ,
,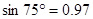 ,
,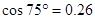 ,
,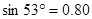 ,
,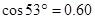 ,
, 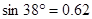 ,
,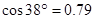
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com