
【題目】在△![]() 中,已知
中,已知![]() ,直線
,直線![]() 經過點
經過點![]() .
.
(Ⅰ)若直線![]() :
:![]() 與線段
與線段![]() 交于點
交于點![]() ,且
,且![]() 為△
為△![]() 的外心,求△
的外心,求△![]() 的外接圓的方程;
的外接圓的方程;
(Ⅱ)若直線![]() 方程為
方程為![]() ,且△
,且△![]() 的面積為
的面積為![]() ,求點
,求點![]() 的坐標.
的坐標.
 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:
【題目】甲罐中有3個紅球,2個白球和3個黑球,乙罐中有5個紅球,3個白球和3個黑球.先從甲罐中隨機取出一球放入乙罐,分別以![]() ,
,![]() 和
和![]() 表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以
表示由甲罐取出的球是紅球,白球和黑球的事件;再從乙罐中隨機取出一球,以![]() 表示由乙罐取出的球是紅球的事件,則下列結論中正確的是__________(寫出所有正確結論的序號).
表示由乙罐取出的球是紅球的事件,則下列結論中正確的是__________(寫出所有正確結論的序號).
①P(B)=![]() ;②
;②![]() ;
;
③事件B與事件A1相互獨立;
④A1,A2,A3是兩兩互斥的事件;
⑤P(B)的值不能確定,因為它與A1,A2,A3中究竟哪一個發生有關.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣mx(m∈R).
(1)討論函數f(x)的單調區間;
(2)當m≥ ![]() 時,設g(x)=2f(x)+x2的兩個極值點x1 , x2(x1<x2)恰為h(x)=lnx﹣cx2﹣bx的零點,求y=(x1﹣x2)h′(
時,設g(x)=2f(x)+x2的兩個極值點x1 , x2(x1<x2)恰為h(x)=lnx﹣cx2﹣bx的零點,求y=(x1﹣x2)h′( ![]() )的最小值.
)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正方體ABCDA1B1C1D1中,O為底面ABCD的中心,P,Q分別為![]() 的中點.
的中點.
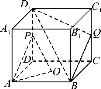
求證:(1)平面D1 BQ∥平面PAO.
(2)求異面直線QD1與AO所成角的余弦值;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊平行四邊形綠地ABCD,經測量BC=2百米,CD=1百米,∠BCD=120°,擬過線段BC上一點E設計一條直路EF(點F在四邊形ABCD的邊上,不計路的寬度),將綠地分為面積之比為1:3的左右兩部分,分別種植不同的花卉,設EC=x百米,EF=y百米. 
(1)當點F與點D重合時,試確定點E的位置;
(2)試求x的值,使路EF的長度y最短.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人在一次射擊比賽中各射靶5次,兩人成績的條形統計圖如圖所示,則( ) 
A.甲的成績的平均數小于乙的成績的平均數
B.甲的成績的中位數等于乙的成績的中位數
C.甲的成績的方差小于乙的成績的方差
D.甲的成績的極差小于乙的成績的極差
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=aex+ ![]() +b(a>0).
+b(a>0).
(Ⅰ)求f(x)在[0,+∞)內的最小值;
(Ⅱ)設曲線y=f(x)在點(2,f(2))處的切線方程為y= ![]() ,求a,b的值.
,求a,b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 則一定有( )
則一定有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】本題主要考查不等關系。已知![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 。故選
。故選![]()
【題型】單選題
【結束】
5
【題目】關于x的不等式ax2+bx+2>0的解集為{x|-1<x<2},則關于x的不等式bx2-ax-2>0的解集為( )
A. {x|-2<x<1} B. {x|x>1或x<-2}
C. {x|x>2或x<-1} D. {x|x<-1或x>1}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,求點D的坐標;
,求點D的坐標;
(2)問是否存在實數α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,說明理由.
成立?若存在,求出α,β的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com