
【題目】定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,且
,且![]() .當
.當![]() 時,
時, ![]() .
.
(1)求![]() 在
在![]() 上的解析式;
上的解析式;
(2)證明![]() 在
在![]() 上是減函數;
上是減函數;
(3)當![]() 取何值時,方程
取何值時,方程![]() 在
在![]() 上有解.
上有解.
【答案】(1) ;(2)見解析;(3)
;(2)見解析;(3)![]() ,或
,或![]() ,或
,或![]() .
.
【解析】試題分析:(1)設![]() ,則
,則![]() 結合f(-x)=-f(x),及x∈(0,1)時,
結合f(-x)=-f(x),及x∈(0,1)時, ![]() ,,可求x∈(-1,0)時得f(x),在f(-x)=-f(x)中可求f(0)=0
,,可求x∈(-1,0)時得f(x),在f(-x)=-f(x)中可求f(0)=0
(2)利用函數的單調性的定義證明即可.
(3)方程![]() 在
在![]() 上有解的充要條件是,
上有解的充要條件是, ![]() 在函數
在函數![]() ,
, ![]() 的值域內取值,只需求出函數的值域,然后求解k的范圍.
的值域內取值,只需求出函數的值域,然后求解k的范圍.
試題解析:
(1)設![]() ,則
,則![]() .
.
∵![]() ,且
,且![]() 時,
時, ![]() ,
,
∴![]() 時,有
時,有![]() .
.
在![]() 中,令
中,令![]() 得
得
![]() .
.
∵![]() ,
, ![]() ,令
,令![]() ,
,
得![]() ,
,
∴![]() ,從而
,從而![]() ,
,
∴當![]() 時,有
時,有
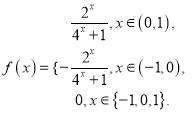 .
.
(2)設![]() ,則
,則![]() ,
,
![]()
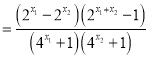 .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
, ![]() .
.
又∵![]() ,
,
∴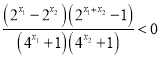 ,
,
即![]() ,∴
,∴![]() 在
在![]() 上是減函數.
上是減函數.
(3)方程![]() 在
在![]() 上有解的充要條件是,
上有解的充要條件是, ![]() 在函數
在函數![]() ,
, ![]() 的值域內取值.
的值域內取值.
∵![]() 時,
時, ![]() 是減函數,
是減函數,
∴![]() 時,
時, ![]() ,
,
即![]() .
.
∵![]() ,∴
,∴![]() 時,
時,
![]() .
.
又![]() ,
,
∴![]() 時,函數
時,函數![]() 的值域為
的值域為![]() .
.
∴當![]() ,或
,或![]() ,或
,或![]() 時,方程
時,方程![]() 在
在![]() 上有解.
上有解.


科目:高中數學 來源: 題型:
【題目】為調查大學生這個微信用戶群體中每人擁有微信群的數量,現從武漢市大學生中隨機抽取100位同學進行了抽樣調查,結果如下:
微信群數量 | 頻數 | 頻率 |
0至5個 | 0 | 0 |
6至10個 | 30 | 0.3 |
11至15個 | 30 | 0.3 |
16至20個 | a | c |
20個以上 | 5 | b |
合計 | 100 | 1 |
(Ⅰ)求a,b,c的值;
(Ⅱ)以這100個人的樣本數據估計武漢市的總體數據且以頻率估計概率,若從全市大學生(數量很大)中隨機抽取3人,記X表示抽到的是微信群個數超過15個的人數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設[x]表示不超過x的最大整數,如:[π]=3,[﹣4.3]=﹣5.給出下列命題: ①對任意實數x,都有[x]﹣x≤0;
②若x1≤x2 , 則[x1]≤[x2];
③[lg1]+[lg2]+[lg3]+…+[lg100]=90;
④若函數f(x)= ![]() ﹣
﹣ ![]() ,則y=[f(x)]+[f(﹣x)]的值域為{﹣1,0}.
,則y=[f(x)]+[f(﹣x)]的值域為{﹣1,0}.
其中所有真命題的序號是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在長方體ABCD﹣A1B1C1D1中,底面ABCD是邊長為 ![]() 的正方形,AA1=3,E是AA1的中點,過C1作C1F⊥平面BDE與平面ABB1A1交于點F,則
的正方形,AA1=3,E是AA1的中點,過C1作C1F⊥平面BDE與平面ABB1A1交于點F,則 ![]() =
=
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知極點與直角坐標系的原點重合,極軸與x軸的正半軸重合,圓C的極坐標是ρ=2asinθ,直線l的參數方程是  (t為參數).
(t為參數).
(1)若a=2,M為直線l與x軸的交點,N是圓C上一動點,求|MN|的最大值;
(2)若直線l被圓C截得的弦長為 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(文科)設函數f(x)=x2﹣2ax﹣8a2(a>0),記不等式f(x)≤0的解集為A.
(1)當a=1時,求集合A;
(2)若(﹣1,1)A,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求函數f(x)在[t,t+2](t>0)上的最小值;
(2)對一切x∈(0,+∞),2f(x)≥g(x)恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設S={x|x=m+n![]() ,m、n∈Z}.
,m、n∈Z}.
(1)若a∈Z,則a是否是集合S中的元素?
(2)對S中的任意兩個x1、x2,則x1+x2、x1·x2是否屬于S?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com