
【題目】已知函數![]() .
.
(1)若![]() ,求函數
,求函數![]() 的極值;
的極值;
(2)若函數![]() 有兩個零點,求實數
有兩個零點,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 時,
時, ![]() 取極大值
取極大值![]() ;當
;當![]() 時,
時, ![]() 取極小值
取極小值![]() ;(2)實數
;(2)實數![]() 的取值范圍是
的取值范圍是![]() 。
。
【解析】試題分析:(1)函數求導得![]() ,討論導數的單調性即可得極值;
,討論導數的單調性即可得極值;
(2)函數求導得![]() ,討論
,討論![]() ,
, ![]() ,
, ![]() 和
和![]() 時函數的單調性及最值即可下結論.
時函數的單調性及最值即可下結論.
試題解析:
(1)函數定義域為![]() ,
, ![]() .
.
![]() ,解得
,解得![]() ,
, ![]() ,
,
列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 極大值 |
| 極小值 |
|
所以![]() 時,
時, ![]() 取極大值
取極大值![]() ;當
;當![]() 時,
時, ![]() 取極小值
取極小值![]() .
.
(2)![]() ,
,
當![]() 時,易知函數
時,易知函數![]() 只有一個零點,不符合題意;
只有一個零點,不符合題意;
當![]() 時,在
時,在![]() 上,
上, ![]() ,
, ![]() 單調遞減;
單調遞減;
在![]() 上,
上, ![]() ,
, ![]() 單調遞增;
單調遞增;
![]() ,且
,且![]() ,
, ![]() →
→![]() ,
, ![]() →
→![]() ,
,
所以函數![]() 有兩個零點.
有兩個零點.
當![]() 時,在
時,在![]() 和
和![]() 上,
上, ![]() ,
, ![]() 單調遞增;在
單調遞增;在![]() 上
上![]() ,
, ![]() 單調遞減;
單調遞減;
![]() ,函數
,函數![]() 至多有一個零點,不符合題意.
至多有一個零點,不符合題意.
當![]() 時,在
時,在![]() 和
和![]() 上
上![]() ,
, ![]() 單調遞增;在
單調遞增;在![]() 上
上![]() ,
, ![]() 單調遞減;
單調遞減;
![]() ,函數
,函數![]() 至多有一個零點,不符合題意.
至多有一個零點,不符合題意.
綜上:實數![]() 的取值范圍是
的取值范圍是![]() .
.


科目:高中數學 來源: 題型:
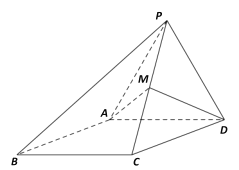
【題目】如圖,四棱錐![]() ,側面
,側面![]() 是邊長為2的正三角形,且與底面垂直,底面
是邊長為2的正三角形,且與底面垂直,底面![]() 是
是![]() 的菱形,
的菱形, ![]() 為棱
為棱![]() 上的動點,且
上的動點,且![]() .
.
(I)求證: ![]() 為直角三角形;
為直角三角形;
(II)試確定![]() 的值,使得二面角
的值,使得二面角![]() 的平面角余弦值為
的平面角余弦值為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某紡紗廠生產甲、乙兩種棉紗,已知生產甲種棉紗1噸需耗一級籽棉2噸、二級籽棉1噸;生產乙種棉紗1噸需耗一級籽棉1噸,二級籽棉2噸.每1噸甲種棉紗的利潤為900元,每1噸乙種棉紗的利潤為600元.工廠在生產這兩種棉紗的計劃中,要求消耗一級籽棉不超過250噸,二級籽棉不超過300噸.問甲、乙兩種棉紗應各生產多少噸,能使利潤總額最大?并求出利潤總額的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】 (本小題滿分12分)
如圖, 在四面體ABOC中, ![]() , 且
, 且![]() .
.
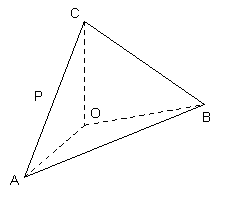
(Ⅰ)設為![]() 為
為![]() 的中點, 證明: 在
的中點, 證明: 在![]() 上存在一點
上存在一點![]() ,使
,使![]() ,并計算
,并計算![]() ;
;
(Ⅱ)求二面角![]() 的平面角的余弦值。
的平面角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位用2160萬元購得一塊空地,計劃在該地塊上建造一棟至少10層,每層2000平方米的樓房.經測算,如果將樓房建為x(x≥10)層,則每平方米的平均建筑費用為560+48x(單位:元).
(1)寫出樓房平均綜合費用y關于建造層數x的函數關系式;
(2)該樓房應建造多少層時,可使樓房每平方米的平均綜合費用最少?最少值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
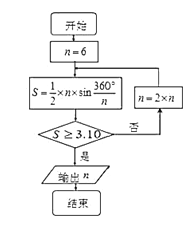
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出
,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出![]() 的值為 ( )
的值為 ( )
(參考數據:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
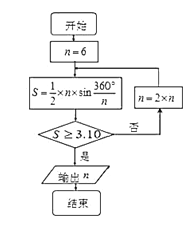
【題目】公元263年左右,我國數學家劉徽發現當圓內接正多邊形的邊數無限增加時,多邊形面積可無限逼近圓的面積,并創立了“割圓術”,利用“割圓術”劉徽得到了圓周率精確到小數點后兩位的近似值![]() ,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出
,這就是著名的“徽率”,如圖是利用劉徽的“割圓術”思想設計的一個程序框圖,則輸出![]() 的值為 ( )
的值為 ( )
(參考數據:![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4![]() 4:坐標系與參數方程
4:坐標系與參數方程
在平面直角坐標系![]() 中,圓C的參數方程為
中,圓C的參數方程為 ,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線
,(t為參數),在以原點O為極點,x軸的非負半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,A,B兩點的極坐標分別為
,A,B兩點的極坐標分別為![]() .
.
(Ⅰ)求圓C的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)點P是圓C上任一點,求△PAB面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com