
【題目】在直角坐標系xOy中,圓C的參數(shù)方程![]() (φ為參數(shù)).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(φ為參數(shù)).以O為極點,x軸的非負半軸為極軸建立極坐標系.
(Ⅰ)求圓C的極坐標方程;
(Ⅱ)直線l的極坐標方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射線OM:θ=
, 射線OM:θ=![]() 與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
與圓C的交點為O,P,與直線l的交點為Q,求線段PQ的長.
【答案】解:(I)圓C的參數(shù)方程![]() (φ為參數(shù)).消去參數(shù)可得:(x﹣1)2+y2=1.
(φ為參數(shù)).消去參數(shù)可得:(x﹣1)2+y2=1.
把x=ρcosθ,y=ρsinθ代入化簡得:ρ=2cosθ,即為此圓的極坐標方程.
(II)如圖所示,由直線l的極坐標方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() ,射線OM:θ=
,射線OM:θ=![]() .
.
可得普通方程:直線ly+![]() x=3
x=3![]() ,射線OMy=
,射線OMy=![]() x.
x.
聯(lián)立![]() ,解得
,解得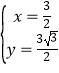 ,即Q
,即Q![]() .
.
聯(lián)立![]() ,解得
,解得![]() 或
或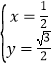 .
.
∴P![]() .
.
∴|PQ|=![]() =2.
=2.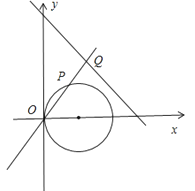
【解析】(I)圓C的參數(shù)方程![]() (φ為參數(shù)).消去參數(shù)可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化簡即可得到此圓的極坐標方程.
(φ為參數(shù)).消去參數(shù)可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化簡即可得到此圓的極坐標方程.
(II)由直線l的極坐標方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射線OM:θ=
, 射線OM:θ=![]() . 可得普通方程:直線lly+
. 可得普通方程:直線lly+![]() x=3
x=3![]() , 射線OMy=
, 射線OMy=![]() x.分別與圓的方程聯(lián)立解得交點,再利用兩點間的距離公式即可得出.
x.分別與圓的方程聯(lián)立解得交點,再利用兩點間的距離公式即可得出.


科目:高中數(shù)學 來源: 題型:
【題目】(1)寫出下列兩組誘導公式:
①關于![]() 與
與![]() 的誘導公式;
的誘導公式;
②關于![]() 與
與![]() 的誘導公式.
的誘導公式.
(2)從上述①②兩組誘導公式中任選一組,用任意角的三角函數(shù)定義給出證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為
的定義域為![]() ,且對任意的
,且對任意的![]() 有
有![]() . 當
. 當![]() 時,
時,![]() ,
,![]() .
.
(1)求![]() 并證明
并證明![]() 的奇偶性;
的奇偶性;
(2)判斷![]() 的單調性并證明;
的單調性并證明;
(3)求![]() ;若
;若![]() 對任意
對任意![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,已知一個八面體的各條棱長為1,四邊形ABCD為正方形,下列說法

①該八面體的體積為![]() ;
;
②該八面體的外接球的表面積為![]() ;
;
③E到平面ADF的距離為![]() ;
;
④EC與BF所成角為60°;
其中不正確的個數(shù)為
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的定義域為(0,+
的定義域為(0,+![]() ),若
),若![]() 在(0,+
在(0,+![]() )上為增函數(shù),則稱
)上為增函數(shù),則稱![]() 為“一階比增函數(shù)”;若
為“一階比增函數(shù)”;若![]() 在(0,+
在(0,+![]() )上為增函數(shù),則稱
)上為增函數(shù),則稱![]() 為”二階比增函數(shù)”。我們把所有“一階比增函數(shù)”組成的集合記為
為”二階比增函數(shù)”。我們把所有“一階比增函數(shù)”組成的集合記為![]() 1,所有“二階比增函數(shù)”組成的集合記為
1,所有“二階比增函數(shù)”組成的集合記為![]() 2。
2。
(1)已知函數(shù)![]() ,若
,若![]() ∈
∈![]() 1,求實數(shù)
1,求實數(shù)![]() 的取值范圍,并證明你的結論;
的取值范圍,并證明你的結論;
(2)已知0<a<b<c,![]() ∈
∈![]() 1且
1且![]() 的部分函數(shù)值由下表給出:
的部分函數(shù)值由下表給出:
|
|
|
|
|
|
|
| t | 4 |
求證:![]() ;
;
(3)定義集合![]() ,且存在常數(shù)k,使得任取x∈(0,+
,且存在常數(shù)k,使得任取x∈(0,+![]() ),
),![]() <k},請問:是否存在常數(shù)M,使得任意的
<k},請問:是否存在常數(shù)M,使得任意的![]() ∈
∈![]() ,任意的x∈(0,+
,任意的x∈(0,+![]() ),有
),有![]() <M成立?若存在,求出M的最小值;若不存在,說明理由。
<M成立?若存在,求出M的最小值;若不存在,說明理由。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2018年3月山東省高考改革實施方案發(fā)布:2020年夏季高考開始全省高考考生總成績將由語文、數(shù)學、外語三門統(tǒng)一高考成績和學生自主選擇的普通高中學業(yè)水平等級性考試科目的成績共同構成.省教育廳為了解正就讀高中的學生家長對高考改革方案所持的贊成態(tài)度,隨機從中抽取了100名城鄉(xiāng)家長作為樣本進行調查,調查結果顯示樣本中有25人持不贊成意見.右面是根據(jù)樣本的調查結果繪制的等高條形圖.

(Ⅰ)請根據(jù)已知條件與等高條形圖完成下面的![]() 列聯(lián)表:
列聯(lián)表:
贊成 | 不贊成 | 合計 | |
城鎮(zhèn)居民 | |||
農村居民 | |||
合計 |
(Ⅱ)試判斷我們是否有95%的把握認為“贊成高考改革方案與城鄉(xiāng)戶口有關”?.
【附】![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD中,底面ABCD為菱形,且PA=PD=DA=2,∠BAD=60°
(I)求證:PB⊥AD;
(II)若PB=![]() , 求二面角A﹣PD﹣C的余弦值.
, 求二面角A﹣PD﹣C的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某幾何體的三視圖(單位:cm)如圖所示,則此幾何體的表面積是( ) 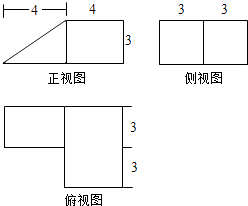
A.90cm2
B.129cm2
C.132cm2
D.138cm2
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com