
【題目】如圖:已知拋物線 C1:y2=2px (p>0),直線 l 與拋物線 C 相交于 A、B 兩點,且當傾斜角為 60°的直線 l 經過拋物線 C1 的焦點 F 時,有|AB|= ![]() .
.
(Ⅰ)求拋物線 C 的方程;
(Ⅱ)已知圓 C2:(x﹣1)2+y2= ![]() ,是否存在傾斜角不為 90°的直線 l,使得線段 AB 被圓 C2 截成三等分?若存在,求出直線 l 的方程;若不存在,請說明理由.
,是否存在傾斜角不為 90°的直線 l,使得線段 AB 被圓 C2 截成三等分?若存在,求出直線 l 的方程;若不存在,請說明理由.
【答案】【解答】(I)當直線l的傾斜角為60°時,直線l的方程為y= ![]() (x﹣
(x﹣ ![]() ),
),
聯立方程組 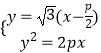 ,消元得3x2﹣5px+
,消元得3x2﹣5px+ ![]() =0,
=0,
∴|AB|= ![]() +p=
+p= ![]() ,解得p=
,解得p= ![]() ,
,
∴拋物線C的方程為y2= ![]() .
.
(II)假設存在直線l,使得AB被圓C2三等分,設直線l與圓C2的交點為C,D,
設直線l的方程為x=my+b,A(x1,y1),B(x2,y2),
聯立方程組  ,得4y2﹣my﹣b=0,
,得4y2﹣my﹣b=0,
∴y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,∴x1+x2=m(y1+y2)+2b=
,∴x1+x2=m(y1+y2)+2b= ![]() +2b,
+2b,
∴AB的中點坐標為M( ![]() +b,
+b, ![]() ),
),
又圓C2的圓心為C2(1,0),∴k ![]() =
= 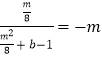 ,
,
即m2+8b﹣7=0,∴b= ![]() .
.
又|AB|= ![]() =
= ![]() .
.
∵圓心C2(1,0)到直線l的距離d= ![]() ,圓C2的半徑為
,圓C2的半徑為 ![]() ,
,
∴|CD|=2 ![]() =
= ![]() ,
,
又|AB|= ![]() =
= ![]() .C,D為AB的三等分點,
.C,D為AB的三等分點,
∴|AB|=3|CD|,
∴ ![]() =
= ![]() ,解得m=±
,解得m=± ![]() ,∴b=
,∴b= ![]() .
.
∴直線l的方程為y=± ![]() x+
x+ ![]() .
.
【解析】(I)聯立方程組,利用根與系數的關系和拋物線的性質列方程解出p;
(II)設直線l的方程為x=my+b,與拋物線方程聯立,求出AB的中點坐標,利用垂徑定理列方程求出m,b的關系。利用弦長公式計算求出|AB|,|CD|,根據|AB|=3|CD|解得m的值和直線l的方程。


科目:高中數學 來源: 題型:
【題目】已知曲線 ![]() 在
在 ![]() 的上方,且曲線
的上方,且曲線 ![]() 上的任意一點到點
上的任意一點到點 ![]() 的距離比到直線
的距離比到直線 ![]() 的距離都小1.
的距離都小1.
(Ⅰ)求曲線 ![]() 的方程;
的方程;
(Ⅱ)設 ![]() ,過點
,過點 ![]() 的直線與曲線
的直線與曲線 ![]() 相交于
相交于 ![]() 兩點.
兩點.
①若 ![]() 是等邊三角形,求實數
是等邊三角形,求實數 ![]() 的值;
的值;
②若 ![]() ,求實數
,求實數 ![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐PABC中,D,E,F分別為棱PC,AC,AB的中點,已知PA⊥AC,PA=6,BC=8,DF=5.求證: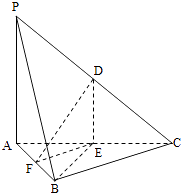
(1)直線PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ) (A>0,ω>0,0<φ<π),其導函數f′(x)的部分圖象如圖所示,則函數f(x)的解析式為( ) 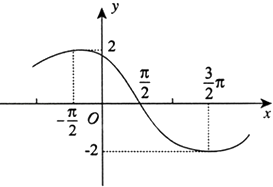
A.f(x)=4sin( ![]() x+
x+ ![]() π)
π)
B.f(x)=4sin( ![]() x+
x+ ![]() )
)
C.f(x)=4sin( ![]() x+
x+ ![]() )
)
D.f(x)=4sin( ![]() x+
x+ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的一段圖象如圖所示:將
的一段圖象如圖所示:將![]() 的圖象向右平移
的圖象向右平移![]() (
(![]() )個單位,可得到函數
)個單位,可得到函數![]() 的圖象,且圖象關于原點對稱.(1)求
的圖象,且圖象關于原點對稱.(1)求![]() 的值.
的值.
(2)求![]() 的最小值,并寫出
的最小值,并寫出![]() 的表達式.
的表達式.
(3)設t>0,關于x的函數![]() 在區間
在區間![]() 上最小值為-2,求t的范圍.
上最小值為-2,求t的范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設F為雙曲線 ![]() ﹣
﹣ ![]() =1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )
=1(a>b>0)的右焦點,過點F的直線分別交兩條漸近線于A,B兩點,OA⊥AB,若2|AB|=|OA|+|OB|,則該雙曲線的離心率為( )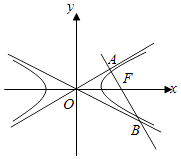
A.![]()
B.2
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+4xsinα+![]() tanα(0<a<
tanα(0<a<![]() )有且僅有一個零點
)有且僅有一個零點
(Ⅰ)求sin2a的值;
(Ⅱ)若cos2β+2sin2β=![]() +sinβ, β∈
+sinβ, β∈![]() ,求β-2α的值
,求β-2α的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,過點P(2,1)的直線l的參數方程為 ![]() (t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ,已知直線l與曲線C交于A、B兩點.
(t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρsin2θ=2cosθ,已知直線l與曲線C交于A、B兩點.
(1)求曲線C的直角坐標方程;
(2)求|PA||PB|的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com