
【題目】已知函數![]() 有兩個零點
有兩個零點![]() 、
、![]() .
.
(1)求實數![]() 的取值范圍;
的取值范圍;
(2)若![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)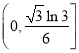 .
.
【解析】
(1)由![]() 得
得![]() ,構造函數
,構造函數![]() ,利用導數分析函數
,利用導數分析函數![]() 的單調性與極值,作出函數
的單調性與極值,作出函數![]() 的圖象,數形結合可得出實數
的圖象,數形結合可得出實數![]() 的取值范圍;
的取值范圍;
(2)由題意推導出![]() ,分
,分![]() 和
和![]() 兩種情況討論,結合
兩種情況討論,結合![]() 以及函數
以及函數![]() 的單調性得出
的單調性得出![]() 的取值范圍,再由
的取值范圍,再由![]() 以及函數
以及函數![]() 的單調性可求得實數
的單調性可求得實數![]() 的取值范圍.
的取值范圍.
(1)![]() ,令
,令![]() ,可得
,可得![]() ,
,
構造函數![]() ,則直線
,則直線![]() 與函數
與函數![]() 的圖象有兩個交點.
的圖象有兩個交點.
![]() ,令
,令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 極大值 |
|
所以,函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ,且在
,且在![]() 處取得極大值
處取得極大值![]() .
.
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,如下圖所示:
,如下圖所示:

如上圖可知,當![]() 時,直線
時,直線![]() 與函數
與函數![]() 的圖象有兩個交點,
的圖象有兩個交點,
因此,實數![]() 的取值范圍是
的取值范圍是![]() ;
;
(2)由(1)可知![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() .
.
①若![]() ,則
,則![]() ,合乎題意;
,合乎題意;
②若![]() ,則
,則![]() ,
,![]() 且函數
且函數![]() 的單調遞減區間為
的單調遞減區間為![]() ,
,
![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() ,此時
,此時![]() .
.
綜上所述,![]() 的取值范圍是
的取值范圍是![]() .
.
![]() 函數
函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,![]() ,即
,即![]() .
.
因此,實數![]() 的取值范圍是
的取值范圍是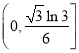 .
.


科目:高中數學 來源: 題型:
【題目】數列![]() :
: ![]() 滿足:
滿足: ![]() .記
.記![]() 的前
的前![]() 項和為
項和為![]() ,并規定
,并規定![]() .定義集合
.定義集合![]() ,
, ![]()
![]() ,
, ![]() .
.
(Ⅰ)對數列![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求集合
,求集合![]() ;
;
(Ⅱ)若集合![]() ,
, ![]() ,證明:
,證明: ![]() ;
;
(Ⅲ)給定正整數![]() .對所有滿足
.對所有滿足![]() 的數列
的數列![]() ,求集合
,求集合![]() 的元素個數的最小值.
的元素個數的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】CPI是居民消費價格指數的簡稱,它是一個反映居民家庭一般所購買的消費品和服務項目價格水平變動情況的宏觀經濟指標.下圖為國家統計局發布的2018年2月-2019年2月全國居民消費價格指數(CPI)數據折線圖(注:同比是今年第n個月與去年第n個月之比;環比表示連續2個單位周期(比如連續兩月)內的量的變化比,環比增長率=(本期數-上期數)/上期數×100%).
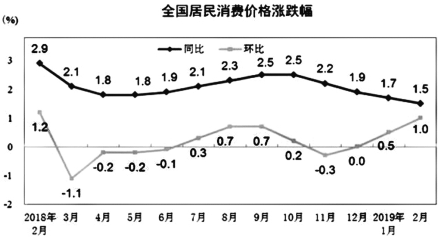
下列說法錯誤的是
A. 2019年2月份居民消費價格同比上漲1.5%B. 2019年2月份居民消費價格環比上漲1.0%
C. 2018年6月份居民消費價格環比下降0.1%D. 2018年11月份居民消費價格同比下降0.3%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,“無樁有站”模式的公共自行車日益普及,即傳統自行車加裝智能鎖,實現掃碼租車及刷卡租車、某公司量產了甲、乙兩種款式的公共自行車并投人使用,為了調查消費者對兩種自行車的租賃情況,現隨機抽取這兩種款式的自行車各100輛,分別統計了每輛車在某周內的出租次數,得到甲、乙兩種自行車這周內出租次數的頻數分布表:
甲 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次數(單位:次) |
|
|
|
|
|
頻數 | 20 | 25 | 25 | 10 | 20 |
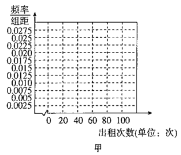
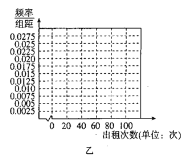
(1)根據頻數分布表,完成上面頻率分布直方圖,并根據頻率分布直方圖比較甲、乙兩種自行車這周內出租次數方差的大小(不必說明理由);
(2)如果兩種自行車每次出租獲得的利潤相同,該公司決定大批量生產其中一種投入某城市使用,請你根據所學的統計知識,給出建議應該生產哪一種自行車,并說明你的理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用計算機生成隨機數表模擬預測未來三天降雨情況,規定1,2,3表示降雨,4,5,6,7,8,9表示不降雨,根據隨機生成的10組三位數:654 439 565 918 288 674 374 968 224 337,則預計未來三天僅有一天降雨的概率為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年,北京將實行新的高考方案.新方案規定:語文數學和英語是考生的必考科目,考生還需從物理化學生物歷史地理和政治六個科目中選取三個科目作為選考科目.若一個學生從六個科目中選出了三個科目作為選考科目,則稱該學生的選考方案確定;否則,稱該學生選考方案待確定,例如,學生甲選擇“物理化學和生物”三個選考科目,則學生甲的選考方案確定,“物理化學和生物”為其選考方案.
某校為了解高一年級840名學生選考科目的意向,隨機選取60名學生進行了一次調查,統計選考科目人數如下表:
性別 | 選考方案確定情況 | 物理 | 化學 | 生物 | 歷史 | 地理 | 政治 |
男生 | 選考方案確定的有16人 | 16 | 16 | 8 | 4 | 2 | 2 |
選考方案待確定的有12人 | 8 | 6 | 0 | 2 | 0 | 0 | |
女生 | 選考方案確定的有20人 | 6 | 10 | 20 | 16 | 2 | 6 |
選考方案待確定的有12人 | 2 | 8 | 10 | 0 | 0 | 2 |
(1)估計該學校高一年級選考方案確定的學生中選考生物的學生有多少人?
(2)從選考方案確定的16名男生中隨機選出2名,求恰好有一人選“物理化學生物”的概率;
(3)從選考方案確定的16名男生中隨機選出2名,設隨機變量 ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的離心率為
的離心率為![]() ,且橢圓
,且橢圓![]() 過點
過點 .過點
.過點![]() 做兩條相互垂直的直線
做兩條相互垂直的直線![]() 、
、![]() 分別與橢圓
分別與橢圓![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四點.
四點.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,
, ![]() ,探究:直線
,探究:直線![]() 是否過定點?若是,請求出定點坐標;若不是,請說明理由.
是否過定點?若是,請求出定點坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓E:![]() (
(![]() )的離心率
)的離心率![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,
,![]() ,過點P的直線斜率為k,交橢圓E于A,B兩點,
,過點P的直線斜率為k,交橢圓E于A,B兩點,![]() .
.
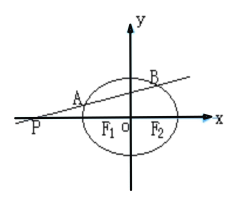
(1)求橢圓E的方程;
(2)設A關于x軸的對稱點為C,證明:三點B、![]() 、C共線;
、C共線;
(3)若點B在一象限,A關于x軸的對稱點為C,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com