【題目】2019年4月20日，重慶市實施高考改革方案，2018年秋季入學的高中一年級的學生將實行“
”模式.即“3”為全國統考科目語文、數學、外語所有學生必考；“1”為物理、歷史科目中選擇一科俗稱“2選1”；“2”為再選學科，考生可在化學、生物、思想政治、地理4個科目中選擇兩科俗稱“4選2”，選擇學科完全相同即為相同“組合”.某校高一年級有三名同學甲，乙，丙根據自己喜歡的大學和專業情況均選擇了物理，為了了解“4選2”選科情況老師找這三名同學來談話情況如下：
甲說：我選了化學，但沒有選思想政治；
乙說：我與甲有一科相同，但沒有選化學和地理；
丙說：我與甲有相同的選科，與乙也有相同選科，但我們三個選的“組合”都不相同.則下列結論正確的是（ ）
A.甲選了化學和地理B.丙可能選化學和思想政治
C.甲一定選地理D.丙一定選了生物和地理
優學名師名題系列答案科目：高中數學 來源： 題型：
【題目】設橢圓
的離心率為
，圓
與
軸正半軸交于點
， 圓
在點處的切線被橢圓
截得的弦長為
.
(1)求橢圓的方程；
(2)設圓上任意一點
處的切線交橢圓于點
、
，求證：
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
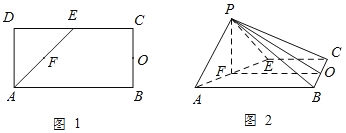
【題目】如圖1，在矩形ABCD中，AB＝4，AD＝2，E，F，O分別為DC，AE，BC的中點．以AE為折痕把△ADE折起，使點D到達點P的位置，且平面PAE⊥平面ABCE（如圖2）．
（Ⅰ）求證：BC⊥平面POF；
（Ⅱ）求直線PA與平面PBC所成角的正弦值；
（Ⅲ）在線段PE上是否存在點M，使得AM∥平面PBC？若存在，求
的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱錐P-ABC中，PA⊥底面ABC，AC⊥BC，H為PC的中點，M為AH中點，PA=AC=2，BC=1．
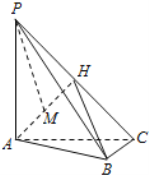
（Ⅰ）求證：AH⊥平面PBC；
（Ⅱ）求PM與平面AHB成角的正弦值；
(Ⅲ)在線段PB上是否存在點N，使得MN∥平面ABC，若存在，請說明點N的位置，若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】 (2017·黃岡質檢)如圖，在棱長均為2的正四棱錐P－ABCD中，點E為PC的中點，則下列命題正確的是( )
A.BE∥平面PAD，且BE到平面PAD的距離為
B.BE∥平面PAD，且BE到平面PAD的距離為
C.BE與平面PAD不平行，且BE與平面PAD所成的角大于30°
D.BE與平面PAD不平行，且BE與平面PAD所成的角小于30°
查看答案和解析>>
科目：高中數學 來源： 題型：
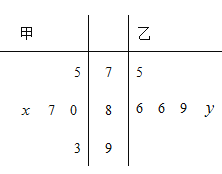
【題目】在學校組織的英語單詞背誦比賽中，5位評委對甲、乙兩名同學的評分如莖葉圖所示（分數為整數，且滿分100分），若甲同學所得評分的中位數為87，乙同學所得評分的唯一眾數為86，則甲同學所得評分的平均數不小于乙同學所得評分的平均數的概率為______．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的個數是（ ）
①一組數據的標準差越大，則說明這組數據越集中；
②曲線
與曲線
的焦距相等；
③在頻率分布直方圖中，估計的中位數左邊和右邊的直方圖的面積相等；
④已知橢圓
，過點
作直線，當直線斜率為
時，M剛好是直線被橢圓截得的弦AB的中點.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
