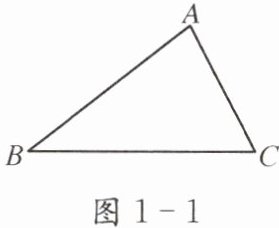
如圖1-1,在△ABC中,從點B出發,沿著三角形的邊到點C,有幾條線路可以選擇? 各條線路的長之間有什么關系? 請說明理由.
答案:【解析】:
本題可根據三角形的三邊關系來分析從點$B$出發沿著三角形的邊到點$C$的線路選擇以及各條線路長之間的關系。
從點$B$出發沿著三角形的邊到點$C$,有兩條線路可以選擇:
線路一:直接從$B$到$C$,線路長為$BC$;
線路二:從$B$經過$A$再到$C$,線路長為$AB + AC$。
根據三角形三邊關系“三角形任意兩邊之和大于第三邊”,在$\triangle ABC$中,$AB$與$AC$是兩邊,$BC$是第三邊,所以$AB + AC>BC$。
【答案】:
解:有兩條線路可以選擇。
線路一:$B\to C$,線路長為$BC$;
線路二:$B\to A\to C$,線路長為$AB + AC$。
因為三角形任意兩邊之和大于第三邊,在$\triangle ABC$中,$AB + AC>BC$。
例 從長度分別為3 cm,4 cm,5 cm,6 cm和9 cm的小木棒中任意取3根,首尾順次相接,能否搭成三角形? 若能,試判斷搭成三角形的形狀.
答案:解:從5根小木棒中任取3根,共有以下10種組合:
1. 3cm,4cm,5cm:3+4>5,3+5>4,4+5>3,能搭成三角形。因為32+42=52,所以是直角三角形。
2. 3cm,4cm,6cm:3+4>6,3+6>4,4+6>3,能搭成三角形。因為32+42=25<62=36,所以是鈍角三角形。
3. 3cm,4cm,9cm:3+4=7<9,不能搭成三角形。
4. 3cm,5cm,6cm:3+5>6,3+6>5,5+6>3,能搭成三角形。因為32+52=34>62=36不成立,32+52=34>62=36不成立,所以是銳角三角形。
5. 3cm,5cm,9cm:3+5=8<9,不能搭成三角形。
6. 3cm,6cm,9cm:3+6=9,不能搭成三角形。
7. 4cm,5cm,6cm:4+5>6,4+6>5,5+6>4,能搭成三角形。因為42+52=41>62=36,所以是銳角三角形。
8. 4cm,5cm,9cm:4+5=9,不能搭成三角形。
9. 4cm,6cm,9cm:4+6>9,4+9>6,6+9>4,能搭成三角形。因為42+62=52<92=81,所以是鈍角三角形。
10. 5cm,6cm,9cm:5+6>9,5+9>6,6+9>5,能搭成三角形。因為52+62=61<92=81,所以是鈍角三角形。
綜上,能搭成三角形的組合及形狀為:
(3,4,5)直角三角形;(3,4,6)鈍角三角形;(3,5,6)銳角三角形;(4,5,6)銳角三角形;(4,6,9)鈍角三角形;(5,6,9)鈍角三角形。
2. 選擇題:
(1)在△ABC中,已知∠A-∠B= 90°,那么△ABC是(
C
).
A. 直角三角形
B. 銳角三角形
C. 鈍角三角形
D. 等邊三角形
(2)下列長度的各組線段中,能組成三角形的是(
D
).
A. 1 cm,2 cm,3 cm
B. 7 cm,5 cm,12 cm
C. 6 cm,3 cm,2 cm
D. 4 cm,5 cm,6 cm
答案:
(1)解:因為∠A - ∠B = 90°,所以∠A = ∠B + 90°,則∠A > 90°,所以△ABC是鈍角三角形,選C。
(2)解:三角形任意兩邊之和大于第三邊。A選項1+2=3,不能組成三角形;B選項7+5=12,不能組成三角形;C選項3+2=5 < 6,不能組成三角形;D選項4+5=9 > 6,4+6=10 > 5,5+6=11 > 4,能組成三角形,選D。


